题目内容
【题目】已知椭圆![]() ,且椭圆C上恰有三点在集合
,且椭圆C上恰有三点在集合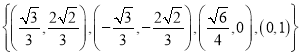 中.
中.
(1)求椭圆C的方程;
(2)若点O为坐标原点,直线AB与椭圆交于A、B两点,且满足![]() ,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
(3)在(2)的条件下,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)点O到直线AB的距离为定值
(2)点O到直线AB的距离为定值![]() (3)
(3)![]()
【解析】
(1)利用椭圆的对称性得椭圆必过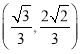 和
和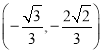 ,结合椭圆过点
,结合椭圆过点![]() ,求得
,求得![]() 的值,从而得到椭圆的方程;
的值,从而得到椭圆的方程;
(2)设![]() ,
,![]() ,对直线的斜率进行讨论,当斜率存在时设为
,对直线的斜率进行讨论,当斜率存在时设为![]() ,
,
由![]() 得
得![]() ,代入点到直线的距离公式可得答案;
,代入点到直线的距离公式可得答案;
(3)将弦![]() 表示成关于
表示成关于![]() 的函数,利用基本不等式求得弦
的函数,利用基本不等式求得弦![]() 的最大值,再代入三角形的面积公式,求得三角形面积的最大值.
的最大值,再代入三角形的面积公式,求得三角形面积的最大值.
(1)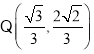 和
和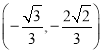 关于原点对称,故由题意知,椭圆C必过此两点
关于原点对称,故由题意知,椭圆C必过此两点
![]() ,又当椭圆过点
,又当椭圆过点![]() 时,
时,![]() ,∴
,∴![]() ,
,
此时满足![]() ,符合题意.
,符合题意.
所以椭圆![]() .
.
又当椭圆过点 时,
时,![]() ,∴
,∴![]() ,
,
此时![]() ,不符合题意.
,不符合题意.
综上:椭圆![]() .
.
(2)设![]() ,
,![]() ,若斜率存在,则设直线
,若斜率存在,则设直线![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
,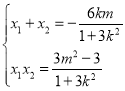
由![]() 知,
知,
![]() ,
,
代入得![]() ,
,
又原点到直线AB的距离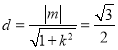 ,
,
且当AB的斜率不存在时,![]() ,可得
,可得![]() ,依然成立.
,依然成立.
所以点O到直线AB的距离为定值![]() .
.
(3)由(2)知,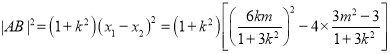
由(2)知,![]() ,
,
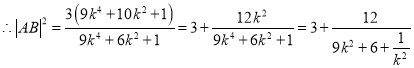 ;
;
因为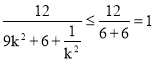 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
所以![]() ;
;
易知当AB斜率不存在时,![]() ,所以
,所以![]() ,
,
综上得![]() 的面积的最大值为
的面积的最大值为![]() .
.

练习册系列答案
相关题目
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.

