题目内容
9．在正方体ABCD-A1B1C1D1中，P为A1C1任意一点．（1）求证：DP∥平面AB1C
（2）求证：平面AB1D1∥平面C1BD．
分析 （1）由已知推导出A1C1∥AC，A1D∥B1C，推导出平面ACB1∥平面A1C1D，由此能证明DP∥平面AB1C．
（2）由已知条件推导出B1D1∥BD，AD1∥BC1，由此能证明平面AB1D1∥平面C1BD．
解答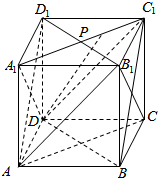 
（1）证明：∵在正方体ABCD-A1B1C1D1中，A1C1∥AC，A1D∥B1C，
A1C1∩A1D=A1，AC∩B1C=C，
A1C1?平面A1C1D，AD1?平面A1C1D，AC?平面ACB1，B1C?平面ACB1，
∴平面ACB1∥平面A1C1D，
∵DP?平面A1C1D，∴DP∥平面AB1C．
（2）∵在正方体ABCD-A1B1C1D1中，B1D1∥BD，AD1∥BC1，
AD1∩B1D1=D1，BD∩BC1=B，
B1D1?平面AB1D1，AD1?平面AB1D1，BD?平面C1BD，BC1?平面C1BD，
∴平面AB1D1∥平面C1BD．
点评 本题考查线面平行、面面平行的证明，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
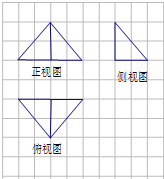
19．某几何体的三视图如图所示，图中方格的长度为1，则该几何体的外接球的体积为（ ）
| A． | $\frac{8}{3}π$ | B． | 8π | C． | $\frac{32}{3}π$ | D． | $\frac{16}{3}π$ |
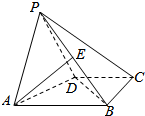如图，在四棱锥P-ABCD中，已知侧面PAD为等腰三角形，底面ABCD为直角梯形，AB∥CD，∠ABC=∠APD=90°，侧面PAD⊥底面ABCD，且AB=4，AP=PD=BC=CD=2．