题目内容
19.某几何体的三视图如图所示,图中方格的长度为1,则该几何体的外接球的体积为( )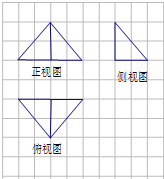
| A. | $\frac{8}{3}π$ | B. | 8π | C. | $\frac{32}{3}π$ | D. | $\frac{16}{3}π$ |
分析 根据几何体的三视图,得出该几何体是底面为等腰三角形,高为2的三棱锥,
结合图形得出该几何体的外接球的半径为2,求出外接球的体积即可.
解答 解:根据几何体的三视图,得;
该几何体是底面为等腰三角形,高为2的三棱锥,
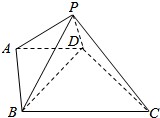
且侧面PAC⊥底面ABC,如图所示:
则DA=DB=DC=DP=2,
∴三棱锥P-ABC的外接球的半径为2,
该三棱锥外接球的体积为V=$\frac{4}{3}$π•23=$\frac{32}{3}$π.
故选:C.
点评 本题考查了空间几何体的三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,并求出外接球的半径,是基础题目.

练习册系列答案
相关题目
4.下列说法中不正确的是( )
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
 直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.
直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.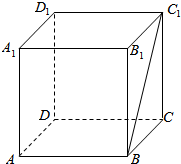
 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.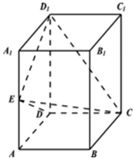 (Ⅰ)证明:A1B1∥平面CDE;
(Ⅰ)证明:A1B1∥平面CDE;