题目内容
1.已知函数f(x)=$\frac{1}{3}$x3+f′(1)x2-x-1,x∈R,其中f′(x)为f(x)的导函数(Ⅰ)若函数f(x)在区间(-a,1+a)上存在极小值点,求实数a的取值范围;
(Ⅱ)设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),若g(t)≥b+t,对任意t∈[-3,-2]恒成立,求实数b的取值范围.
分析 (Ⅰ)求导数f′(x),然后求f′(1),从而得到f′(1)=0,从而得出f(x)=$\frac{1}{3}{x}^{3}-x-1$,f′(x)=x2-1,从而可求得极小值点为x=1,从而可得到$\left\{\begin{array}{l}{-a<1}\\{1+a>1}\end{array}\right.$,这样解出实数a的取值范围即可;
(Ⅱ)由t的范围求出t+3的范围,这样可得到t+3≤1,且-1∈[t,t+3],从而可得出M(t)=f(-1)=-$\frac{1}{3}$,再通过作差比较f(t+3)和f(t)的大小,从而得出m(t)=f(t)=$\frac{1}{3}{t}^{3}-t-1$,从而得出g(t)=$-\frac{1}{3}{t}^{3}+t+\frac{2}{3}$.然后通过求导数,根据导数符号便能判断出g(t)在[-3,-2]上单调递减,从而g(-2)=$\frac{4}{3}$是g(t)的最小值,而b+t在[-3,-2]上的最大值显然为b-2,从而可得出$\frac{4}{3}≥b-2$,这样便可得出实数t的取值范围.
解答 解:(Ⅰ)f′(x)=x2+2f′(1)x-1,∴f′(1)=2f′(1);
∴f′(1)=0;
∴$f(x)=\frac{1}{3}{x}^{3}-x-1$,f′(x)=x2-1;
∴x<-1时,f′(x)>0,-1<x<1时,f′(x)<0,x>1时,f′(x)>0;
∴x=-1是f(x)的极大值点,x=1是f(x)的极小值点;
又f(x)在区间(-a,1+a)上存在极小值点;
∴$\left\{\begin{array}{l}{-a<1}\\{1+a>1}\end{array}\right.$;
∴a>0;
∴实数a的取值范围为(0,+∞);
(Ⅱ)-3≤t≤-2;
∴0≤t+3≤1;
∴-1∈[t,t+3];
∴x=-1f(x)取到最大值M(t)=$-\frac{1}{3}$;
$f(t+3)-f(t)=\frac{1}{3}(t+3)^{3}-(t+3)$$-\frac{1}{3}{t}^{3}+t$=3(t2+3t+2);
设h(t)=3(t2+3t+2),对称轴为t=$-\frac{3}{2}$,在t∈[-3,-2]上单调递减,且h(-2)=0;
∴h(t)≥0;
∴f(t+3)≥f(t);
∴f(x)在[t,t+3]上的最小值m(t)=f(t)=$\frac{1}{3}{t}^{3}-t-1$;
∴$g(t)=M(t)-m(t)=-\frac{1}{3}-\frac{1}{3}{t}^{3}+t+1$=$-\frac{1}{3}{t}^{3}+t+\frac{2}{3}$,g′(t)=-t2+1=-(t+1)(t-1);
∴t∈[-3,-2]时,g′(t)<0;
∴g(t)在[-3,-2]上单调递减;
∴g(t)在[-3,-2]上的最小值为g(-2)=$\frac{4}{3}$,b+t在t∈[-3,-2]上的最大值为b-2;
∵g(t)≥b+t对任意的t∈[-3,-2]恒成立;
∴$\frac{4}{3}≥b-2$;
∴$b≤\frac{10}{3}$;
∴实数b的取值范围为:$(-∞,\frac{10}{3}]$.
点评 考查函数极大值点,极小值点的定义及求法,函数极值的概念及求法,根据导数求函数在闭区间上最值的方法和过程,以及根据导数符号判断函数单调性的方法,以及根据函数的单调性定义求函数的最值.

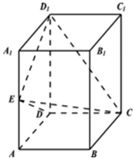 (Ⅰ)证明:A1B1∥平面CDE;
(Ⅰ)证明:A1B1∥平面CDE;