Question

18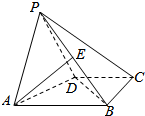．如图，在四棱锥P-ABCD中，已知侧面PAD为等腰三角形，底面ABCD为直角梯形，AB∥CD，∠ABC=∠APD=90°，侧面PAD⊥底面ABCD，且AB=4，AP=PD=BC=CD=2．
（1）求异面直线PA与BD所成角的大小；
（2）设点E在侧棱PB上，若二面角E-AD-C的大小为$\frac{π}{4}$，求BE的长．

Answer 1

分析 （1）在Rt△PAD中，PA=PD=2，可得AD=2$\sqrt{2}$．在直角梯形ABCD中，AB∥CD，∠ABC=∠BCD=90°，可得AD²+DB²=AB²，因此DB⊥AD，利用面面垂直的性质可得：BD⊥平面PAD，即可得出异面直线PA与BD所成角的大小．
（2）如图所示，取AD的中点O，AB的中点M，连接PO，OM．利用等腰三角形的星座与面面垂直的性质定理可得：PO⊥平面ABCD，AO⊥OM．由BD⊥平面PAD，OM∥BD．可得OM⊥AD．建立如图所示的空间直角坐标系．设$\overrightarrow{BE}=λ\overrightarrow{BP}$，则$\overrightarrow{OE}$=$\overrightarrow{OB}+λ\overrightarrow{BP}$．$\overrightarrow{AE}$=$（λ\sqrt{2}-2\sqrt{2}，2\sqrt{2}-2\sqrt{2}λ，\sqrt{2}λ）$．设平面AED的法向量为$\overrightarrow{m}$=（x，y，z），利用$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AE}=0}\\{\overrightarrow{m}•\overrightarrow{AD}=0}\end{array}\right.$，可得$\overrightarrow{m}$．取平面ABCD的法向量$\overrightarrow{n}$=（0，0，1）．利用二面角E-AD-C的大小为$\frac{π}{4}$，可得$cos\frac{π}{4}$=$|cos＜\overrightarrow{m}，\overrightarrow{n}＞|$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$解出λ，即可得出．

解答 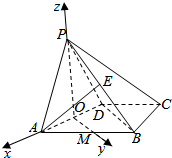解：（1）在Rt△PAD中，PA=PD=2，∴AD=2$\sqrt{2}$．
在直角梯形ABCD中，AB∥CD，∠ABC=∠BCD=90°，
∴BD=$\sqrt{2}BC$=2$\sqrt{2}$，
∵$（2\sqrt{2}）^{2}+（2\sqrt{2}）^{2}={4}^{2}$，
∴∠ADB=90°，∴DB⊥AD，
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴BD⊥平面PAD，∴BD⊥AP．
∴异面直线PA与BD所成角的大小为90°．
（2）如图所示，
取AD的中点O，AB的中点M，连接PO，OM．
由PO⊥AD，侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，
∴PO⊥平面ABCD，
∴AO⊥OM．
∵BD⊥平面PAD，OM∥BD．
∴OM⊥AD．
建立如图所示的空间直角坐标系．
A（$\sqrt{2}$，0，0），B（-$\sqrt{2}$，2$\sqrt{2}$，0）P（0，0，$\sqrt{2}$），D（-$\sqrt{2}$，0，0）．
$\overrightarrow{AD}$=$（-2\sqrt{2}，0，0）$，$\overrightarrow{BP}$=$（\sqrt{2}，-2\sqrt{2}，\sqrt{2}）$．
设$\overrightarrow{BE}=λ\overrightarrow{BP}$，则$\overrightarrow{OE}$=$\overrightarrow{OB}+λ\overrightarrow{BP}$=$（λ\sqrt{2}-\sqrt{2}，2\sqrt{2}-2\sqrt{2}λ，\sqrt{2}λ）$．
$\overrightarrow{AE}$=$（λ\sqrt{2}-2\sqrt{2}，2\sqrt{2}-2\sqrt{2}λ，\sqrt{2}λ）$．
设平面AED的法向量为$\overrightarrow{m}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AE}=0}\\{\overrightarrow{m}•\overrightarrow{AD}=0}\end{array}\right.$，化为$\left\{\begin{array}{l}{（λ-2）\sqrt{2}x+2\sqrt{2}（1-λ）y+\sqrt{2}λz=0}\\{-2\sqrt{2}x=0}\end{array}\right.$，
取$\overrightarrow{m}$=$（0，1，\frac{2λ-2}{λ}）$，
取平面ABCD的法向量$\overrightarrow{n}$=（0，0，1）．
∵二面角E-AD-C的大小为$\frac{π}{4}$，
∴$cos\frac{π}{4}$=$|cos＜\overrightarrow{m}，\overrightarrow{n}＞|$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{|\frac{2λ-2}{λ}|}{\sqrt{1+（\frac{2λ-2}{λ}）^{2}}}$，（0＜λ≤1）．
化为2-2λ=λ，
解得$λ=\frac{2}{3}$．
∴|$\overrightarrow{BE}$|=$\frac{2}{3}$|$\overrightarrow{BP}$|=$\frac{2}{3}$$\sqrt{（\sqrt{2}）^{2}+（-2\sqrt{2}）^{2}+（\sqrt{2}）^{2}}$=$\frac{4\sqrt{3}}{3}$．

点评 本题考查了空间线面位置关系、空间角、向量夹角公式、勾股定理的逆定理、等腰三角形的性质，考查了推理能力与计算能力，属于中档题．