题目内容
14.四边形ABCD是矩形,P为平面ABCD外一点,PA⊥平面ABCD,且PA=AB,则二面角P-BC-D的大小为45°.分析 由已知条件推导出BC⊥平面PAB,从而得到二面角P-BC-D的平面角为∠PBA,由此能求出二面角P-BC-D的大小.
解答 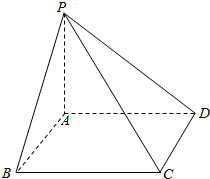 解:∵PA⊥平面ABCD,∴PA⊥BC,
解:∵PA⊥平面ABCD,∴PA⊥BC,
又∵ABCD为矩形,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB,
∵PA?平面PAB,∴BC⊥PA,
又CD⊥BC,∴二面角P-BC-D的平面角即为PA与CD的夹角,
又矩形ABCD,∴CD∥AB,∴∠PBA即为所求的角
∵PA⊥AB,PA=AB,∴∠PBA=45°
即二面角P-BC-D的大小为45°.
故答案为:45°.
点评 本题考查二面角的大小的求法,是中档题,解题时要注意是思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列说法中不正确的是( )
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
3.设F2(c,0)(c>0)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,M是双曲线左支上的一点,线段MF2与圆x2+y2-$\frac{2c}{3}$x+$\frac{{a}^{2}}{9}$=0相切于D,且|MF2|=3|DF2|,则双曲线Γ的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
 如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点
如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点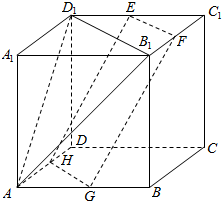 在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH.