题目内容
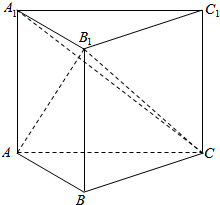
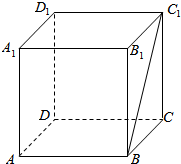
17.直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,边长为2,侧棱A1A=3,M、N分别为A1B1、A1D1的中点,E、F分别是B1C1、C1D1的中点.(1)求证:平面AMN∥平面EFDB;
(2)求平面AMN与平面EFDB的距离.
分析 (1)连接B1D1,NF,证明MN∥平面EFDB,AN∥平面EFDB,即可证明平面AMN∥平面EFDB;
(2)平面AMN与平面EFDB的距离=B到平面AMN的距离h,利用等体积求平面AMN与平面EFDB的距离.
解答  (1)证明:连接B1D1,NF
(1)证明:连接B1D1,NF
∵M、N分别为A1B1、A1D1的中点,E、F分别是B1C1、C1D1的中点,
∴MN∥EF∥B1D1,
∵MN?平面EFDB,EF?平面EFDB,
∴MN∥平面EFDB,
∵NF平行且等于AB,
∴ABFN是平行四边形,
∴AN∥BF,
∵AN?平面EFDB,BF?平面EFDB,
∴AN∥平面EFDB,
∵AN∩MN=N,
∴平面AMN∥平面EFDB;
(2)解:平面AMN与平面EFDB的距离=B到平面AMN的距离h.
△AMN中,AM=AN=$\sqrt{10}$,MN=$\sqrt{2}$,S△AMN=$\frac{1}{2}•\sqrt{2}•\sqrt{10-\frac{1}{2}}$=$\frac{\sqrt{19}}{2}$,
∴由等体积可得$\frac{1}{3}•\frac{\sqrt{19}}{2}h=\frac{1}{3}•\frac{1}{2}•2•2•3$,
∴h=$\frac{12\sqrt{19}}{19}$.
点评 本题考查线面、面面平行的判定,考查平面与平面间距离的计算,属于中档题.

练习册系列答案
相关题目
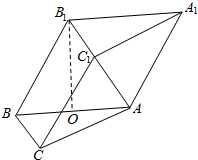 如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点
如图,在棱柱ABC-A1B1C1中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°,顶点为B1在底面ABC上的射影O恰好是AB的中点