题目内容
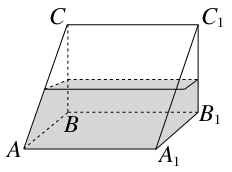
已知等腰梯形PDCB中(如图),PB=3,DC=1,PD=BC= ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
(1)证明:平面PAD⊥平面PCD.
(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
(3)在M满足(2)的情况下,判断直线PD是否平行平面AMC.

 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).(1)证明:平面PAD⊥平面PCD.
(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
(3)在M满足(2)的情况下,判断直线PD是否平行平面AMC.

(1)见解析 (2)M为线段PB的中点时 (3)不平行
(1)因为PDCB为等腰梯形,PB=3,DC=1,PA=1,则PA⊥AD,CD⊥AD.
又因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD?面ABCD,故CD⊥面PAD.
又因为CD?面PCD,所以平面PAD⊥平面PCD.
(2)所求的点M即为线段PB的中点.
证明如下:
设三棱锥M-ACB的高为h1,四棱锥P-ABCD的高为h2,
当M为线段PB的中点时,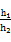 =
=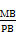 =
= ,
,
所以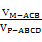 =
=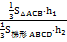 =
=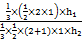 =
= ,所以截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
,所以截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
(3)当M为线段PB的中点时,直线PD与面AMC不平行.
证明如下:(反证法)假设PD∥面AMC,
连接DB交AC于点O,连接MO.
因为PD?面PBD,且面AMC∩面PBD=MO,
所以PD∥MO.
因为M为线段PB的中点时,则O为线段BD的中点,即 =
= ,
,
而AB∥DC,故 =
=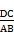 =
= ,故矛盾.
,故矛盾.
所以假设不成立,故当M为线段PB的中点时,直线PD与平面AMC不平行.
又因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD?面ABCD,故CD⊥面PAD.
又因为CD?面PCD,所以平面PAD⊥平面PCD.
(2)所求的点M即为线段PB的中点.
证明如下:
设三棱锥M-ACB的高为h1,四棱锥P-ABCD的高为h2,
当M为线段PB的中点时,
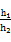 =
=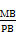 =
= ,
,所以
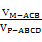 =
=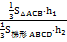 =
=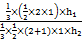 =
= ,所以截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
,所以截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.(3)当M为线段PB的中点时,直线PD与面AMC不平行.
证明如下:(反证法)假设PD∥面AMC,
连接DB交AC于点O,连接MO.
因为PD?面PBD,且面AMC∩面PBD=MO,
所以PD∥MO.
因为M为线段PB的中点时,则O为线段BD的中点,即
 =
= ,
,而AB∥DC,故
 =
=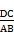 =
= ,故矛盾.
,故矛盾.所以假设不成立,故当M为线段PB的中点时,直线PD与平面AMC不平行.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
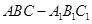 中,平面
中,平面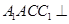 平面ABC,
平面ABC,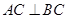 ,
,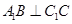 ,
,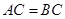 .
.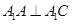 ;
;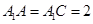 ,求三棱锥
,求三棱锥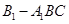 的体积.
的体积.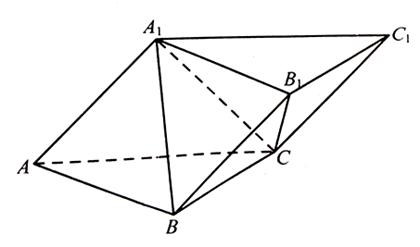
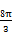
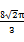
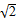 π
π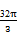
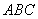 中,
中, 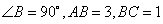 ,以边
,以边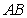 所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )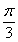
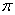
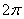
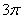
 及其内部一动点
及其内部一动点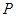 ,集合
,集合 ,则集合
,则集合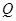 构成的几何体表面积为 .
构成的几何体表面积为 .