题目内容
在斜三棱柱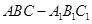 中,平面
中,平面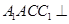 平面ABC,
平面ABC,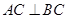 ,
,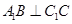 ,
,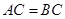 .
.
(1)求证: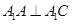 ;
;
(2)若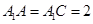 ,求三棱锥
,求三棱锥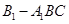 的体积.
的体积.
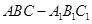 中,平面
中,平面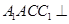 平面ABC,
平面ABC,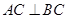 ,
,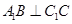 ,
,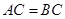 .
.(1)求证:
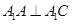 ;
;(2)若
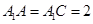 ,求三棱锥
,求三棱锥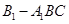 的体积.
的体积.
(1)证明过程详见解析;(2)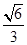 .
.
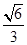 .
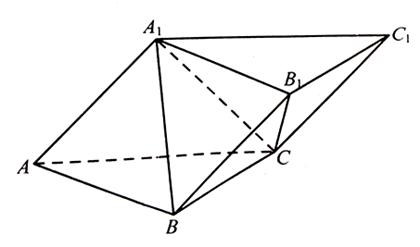
.试题分析:本题主要考查线线垂直、线面垂直、面面垂直、线线平行、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,利用面面垂直的性质得BC⊥平面A1ACC1,则利用线面垂直的性质得A1A⊥BC,由A1B⊥C1C,利用平行线A1A∥C1C,则A1A⊥A1B,利用线面垂直的判定得A1A⊥平面A1BC,则利用线面垂直的性质得A1A⊥A1C;第二问,由于
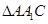 为等腰三角形,平面. A1ACC1⊥平面ABC,所以
为等腰三角形,平面. A1ACC1⊥平面ABC,所以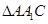 中边AC上的高为斜三棱柱
中边AC上的高为斜三棱柱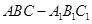 的高,而三棱锥
的高,而三棱锥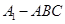 与三棱锥
与三棱锥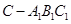 的体积相等.
的体积相等.(1)因为平面A1ACC1⊥平面ABC,AC⊥BC,所以BC⊥平面A1ACC1,
所以A1A⊥BC.
因为A1B⊥C1C,A1A∥C1C,所以A1A⊥A1B,又BC∩A1B=B,
所以A1A⊥平面A1BC,又A1CÌ平面A1BC,所以A1A⊥A1C. 5分
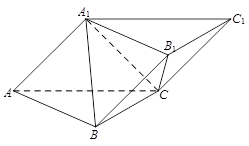
(2)由已知及(1),△A1AC是等腰直角三角形,AA1=A1C=2,AC=
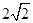 .
.因为平面A1ACC1⊥平面ABC,
所以Rt△A1AC斜边上的高等于斜三棱柱ABC-A1B1C1的高,且等于
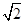 . 7分
. 7分在Rt△ABC中,AC=BC=
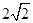 ,S△ABC=
,S△ABC=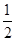 AC·BC=4,
AC·BC=4,三棱柱ABC-A1B1C1的体积V=S△ABC·
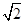 =
=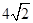 . 10分
. 10分又三棱锥A1-ABC与三棱锥C-A1B1C1的体积相等,都等于
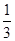 V,
V,所以三棱锥B1-A1BC的体积V1=V-2×
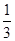 V=
V=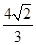 . 12分
. 12分
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
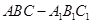 中,
中,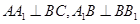 .
.
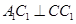 ;
;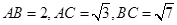 ,问
,问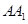 为何值时,三棱柱
为何值时,三棱柱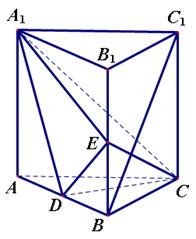
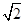 ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积. ,M是线段AE上的动点.
,M是线段AE上的动点.
 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
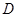 是AC的中点,已知
是AC的中点,已知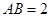 ,
,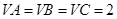 .
. 的体积.
的体积.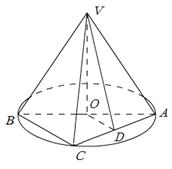
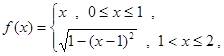 将
将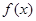 的图像与
的图像与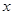 轴围成的封闭图形绕
轴围成的封闭图形绕