题目内容
【题目】已知向量
＝(
sin x，cos x)，
＝(cos x，cos x)，
＝(2，1)．
(1)若∥，求sin xcos x的值；
(2)若0＜x≤
，求函数f(x)＝·的值域．
【答案】（1）
；（2）
【解析】
(1)由向量共线得tan x＝2，再由同角三角函数基本关系得sin xcos x＝
，即可求解；(2)整理f(x)＝
·
＝sin（2x+
）+
，由三角函数性质即可求解最值
(1)∵∥
，∴sin x＝2cos x，tan x＝2.
∴sin xcos x＝
＝=
(2)f(x)＝·＝
sin xcos x＋cos2x
＝
sin 2x＋(1＋cos 2x)=sin（2x+）+
∵0＜x≤
，∴＜2x+≤
.∴
sin（2x+）≤1
∴1≤f(x)≤
.所以f(x)的值域为：
练习册系列答案
阅读快车系列答案
相关题目
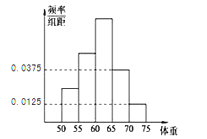
【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价
（单位：元）和销售量
（单位：万件）之间的一组数据，如下表所示：
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量 | 11 | 10 | 8 | 6 | 5 |
（1）根据表中数据，建立关于的回归方程；
（2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在
内，已知该产品的成本是
元/件（其中
），那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）
参考数据：
，
.
参考公式：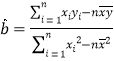
，
.
