题目内容
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求A中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
【答案】(1)A中学至少1名学生入选的概率为![]() .
.
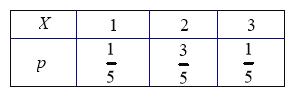
(2)X的分布列为:
X的期望为![]() .
.
【解析】(1)由题意,参加集训的男女生各有6名.
参赛学生全从B中抽取(等价于A中没有学生入选代表队)的概率为![]() .
.
因此,A中学至少1名学生入选的概率为![]() .
.
(2)根据题意,X的可能取值为1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:

因此,X的期望为![]() .
.

练习册系列答案
相关题目