题目内容
【题目】设函数f(x)=|x﹣1|+![]() |x﹣3|
|x﹣3|
(Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若不等式f(x)≤a(x+![]() )的解集非空,求实数a的取值范围.
)的解集非空,求实数a的取值范围.
【答案】解:( I)去绝对值可得f(x)=|x﹣1|+![]() |x﹣3|=
|x﹣3|= ,
,
∴原不等式f(x)>2等价于 或
或 或
或 
解以上不等式组取并集可得原不等式解集为![]() ;
;
( II)f(x)图象如图所示,其中A(1,1),B(3,2),![]() =
=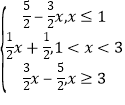 ,直线y=a(x+
,直线y=a(x+![]() )绕点(-
)绕点(-![]() ,0)旋转,
,0)旋转,
由图可得不等式f(x)≤a(x+![]() )的解集非空时,a的范围为
)的解集非空时,a的范围为![]()
【解析】( I)去绝对值可得f(x)= , 可得原不等式f(x)>2等价于
, 可得原不等式f(x)>2等价于 或
或 或
或  , 解不等式组可得;
, 解不等式组可得;
( II)作出f(x)图象,结合图象可得a的取值.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
相关题目