题目内容
11.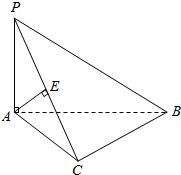 如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:
如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:(1)BC⊥平面PAC;
(2)AE⊥平面PBC;
(3)AE⊥PB.
分析 (1)由PA⊥平面ABC可证PA⊥BC,又∠ACB=90°,即可证明BC⊥平面PAC;
(2)由(1)可证BC⊥AE,又AP=AC,E为PC的中点.可证AE⊥PC,即可证明AE⊥平面PBC.
(3)由(2)知AE⊥平面PBC,PB?平面PBC,即可证明AE⊥PB.
解答 证明:(1)∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
又∵∠ACB=90°,即BC⊥AC,
∴由PA∩AC=A,可得BC⊥平面PAC;
(2)∵由(1)知BC⊥平面PAC,AE?平面PAC,
∴BC⊥AE,
又∵AP=AC,E为PC的中点.
∴AE⊥PC,
∴又PC∩BC=C,可得:AE⊥平面PBC.
(3)∵由(2)知AE⊥平面PBC,PB?平面PBC.
∴AE⊥PB.
点评 本题主要考查了直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.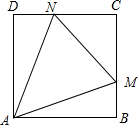 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |