题目内容
16.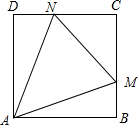 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |
分析 设∠BAM=θ,0<θ<$\frac{π}{4}$,分别由解直角三角形可得AM,AN的长,再由向量的数量积的定义,结合三角函数的恒等变换公式,以及余弦函数的最值,即可得到所求最小值.
解答 解:设∠BAM=θ,0<θ<$\frac{π}{4}$,
在直角△ABM中,AM=$\frac{2}{cosθ}$,
在直角△ADN中,AN=$\frac{2}{cos(\frac{π}{4}-θ)}$,
则$\overrightarrow{AM}$•$\overrightarrow{AN}$=|$\overrightarrow{AM}$|•|$\overrightarrow{AN}$|cos$\frac{π}{4}$
=$\frac{2\sqrt{2}}{cosθcos(\frac{π}{4}-θ)}$=$\frac{4\sqrt{2}}{cos\frac{π}{4}+cos(2θ-\frac{π}{4})}$
=$\frac{4\sqrt{2}}{\frac{\sqrt{2}}{2}+cos(2θ-\frac{π}{4})}$,
当2θ-$\frac{π}{4}$=0,即θ=$\frac{π}{8}$时,cos(2θ-$\frac{π}{4}$)取得最大值1,
则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为$\frac{4\sqrt{2}}{1+\frac{\sqrt{2}}{2}}$=8($\sqrt{2}$-1).
故选:B.
点评 本题考查向量的数量积的定义,考查三角函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
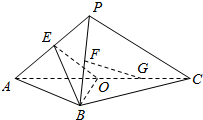 如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).
如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).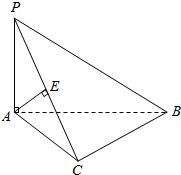 如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:
如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证: