题目内容
2．设函数y=f（x）是偶函数，f′（x）是f（x）的导函数，若f′（x）＞f（x），则下列不等式（e为自然对数的底数）①e2f（2）＜ef（1）＜f（0）；②e-1f（1）＜f（0）＜e2f（2）；③e2f（2）＜f（0）＜e-1f（1）成立的个数有（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 y=f（x）为偶函数，f（-1）=f（1）．构造函数g（x）=exf（-x），研究g（x）的单调性，结合原函数的性质和函数值，即可求解．
解答 解：∵y=f（x）为偶函数，∴f（-1）=f（1）．
构造g（x）=exf（x）=exf（-x），则g′（x）=ex[f（x）-f′（x）]＜0，
∴g（x）=exf（x）单调递减，
∴e2f（2）＜ef（1）＜f（0）；e2f（2）＜f（0）＜e-1f（1）
故选：C．
点评 本题考查函数的奇偶性与单调性，正确构造函数是关键．
练习册系列答案
相关题目
12．不等式6x2-x-1≤0的解集是（ ）
| A． | $[-\frac{1}{2}，\frac{1}{3}]$ | B． | $[\frac{1}{3}，\frac{1}{2}]$ | C． | $[-\frac{1}{3}，\frac{1}{2}]$ | D． | $[-\frac{1}{2}，-\frac{1}{3}]$ |
13．下列各函数中，值域为（0，+∞）的是（ ）
| A． | y=${3^{\frac{1}{x+1}}}$ | B． | y=${2^{-\frac{x}{2}}}$ | C． | y=x2+x+1 | D． | y=$\sqrt{1-{2}^{x}}$ |
14．若三棱锥的三条侧棱两两垂直，且侧棱长都相等，其外接球的表面积是4π，则其侧棱长为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{\sqrt{2}}{3}$ |
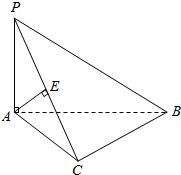如图，已知PA⊥平面ABC，∠ACB=90°，AP=AC，E为PC的中点．求证：