题目内容
6.已知点A($\sqrt{2}$,0),B(-$\sqrt{2}$,0),直线PA与PB的斜率之积为定值-$\frac{1}{2}$.(1)求动点P的轨迹E的方程;
(2)在轨迹E上求一点M,使它到直线l:x-y-2$\sqrt{3}$=0的距离最小.
分析 (1)用坐标表示直线PA与PB的斜率因为直线PA与PB的斜率之积为定值-$\frac{1}{2}$,可得$\frac{y}{x-\sqrt{2}}•\frac{y}{x+\sqrt{2}}=-\frac{1}{2}$,整理得动点P的轨迹E的方程;
(2)设直线y=x+t与轨迹E相切,联立,求出t,即可得出结论.
解答 解:(1)由题意$\frac{y}{x-\sqrt{2}}•\frac{y}{x+\sqrt{2}}=-\frac{1}{2}$,
整理得$\frac{{x}^{2}}{2}+{y}^{2}$=1,所以所求轨迹E的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1(y≠0);
(2)设直线y=x+t与轨迹E相切,联立可得3x2+4tx+2t2-2=0,
∴△=16t2-12(2t2-2)=0,
∴t=$±\sqrt{3}$,
∴t=-$\sqrt{3}$,M($\frac{2\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$)到直线l:x-y-2$\sqrt{3}$=0的距离最小.
点评 本题考查轨迹方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列函数中,在R上是偶函数,且在(0,+∞)上为单调递增函数的是( )
| A. | y=x3 | B. | y=2|x| | C. | y=-x2+1 | D. | y=$\frac{1}{x^2}$ |
14.若三棱锥的三条侧棱两两垂直,且侧棱长都相等,其外接球的表面积是4π,则其侧棱长为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
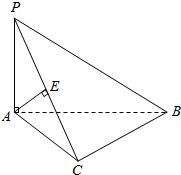 如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:
如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证: