题目内容
3.求y=sin2(x+$\frac{1}{x}$)的导数.分析 利用导数的运算法则、复合函数的导数即可得出.
解答 解:y′=2$sin(x+\frac{1}{x})$$cos(x+\frac{1}{x})$$(x+\frac{1}{x})^{′}$
=$(1-\frac{1}{{x}^{2}})$$sin(2x+\frac{2}{x})$.
点评 本题考查了导数的运算法则、复合函数的导数,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.下列各函数中,值域为(0,+∞)的是( )
| A. | y=${3^{\frac{1}{x+1}}}$ | B. | y=${2^{-\frac{x}{2}}}$ | C. | y=x2+x+1 | D. | y=$\sqrt{1-{2}^{x}}$ |
14.若三棱锥的三条侧棱两两垂直,且侧棱长都相等,其外接球的表面积是4π,则其侧棱长为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
13.已知向量$\overrightarrow{OA}$=(2,-2,3),向量$\overrightarrow{OB}$=(x,1-y,4z),且平行四边形OACB对角线的中点坐标为(0,$\frac{3}{2}$,-$\frac{1}{2}$),则(x,y,z)等于( )
| A. | (-2,-4,-1) | B. | (-2,-4,1) | C. | (-2,4,-1) | D. | (2,-4,-1) |
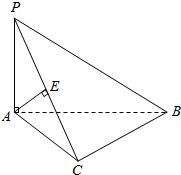 如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:
如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证: