题目内容
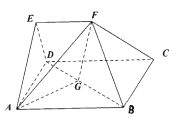
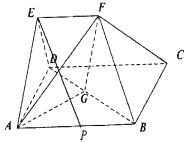
【题目】在多面体![]() 中,四边形
中,四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
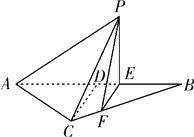
(Ⅰ) 求证: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段![]() 上确定一点
上确定一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)当点![]() 满足
满足![]() 时,平面
时,平面![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
【解析】试题分析:(Ⅰ)在![]() 中,由正弦定理得得
中,由正弦定理得得![]() 即
即![]() 即
即![]() ,在
,在![]() 中,可得
中,可得![]() 即
即![]() ,即
,即![]() ,由此可证明
,由此可证明![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)可得, ![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]()
如图,过![]() 点作平面
点作平面![]() 的垂线
的垂线![]() ,以点
,以点![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,求出相应点及向量的坐标,设平面
轴建立空间直角坐标系,求出相应点及向量的坐标,设平面![]() 的一个法向量
的一个法向量![]() ,令
,令![]() ,得
,得
![]() .
.
易知平面![]() 的一个法向量
的一个法向量![]() .由向量的夹角公式
.由向量的夹角公式
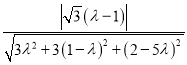
![]() , 化简得
, 化简得![]() ,
, ![]() .
.
即当点![]() 满足
满足![]() 时,平面
时,平面![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
试题解析:(Ⅰ) ![]() 四边形
四边形![]() 是正方形,
是正方形, ![]() .
.
在![]() 中,
中, ![]() ,即
,即![]() 得
得![]()
![]() ,即
,即![]() ,在梯形
,在梯形![]() 中,过
中,过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]()
在![]() 中,可求
中,可求![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]() .
.
又![]() ,
,
![]() 平面
平面![]() ,
,
(Ⅱ)由(Ⅰ)可得, ![]() ,
, ![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]()
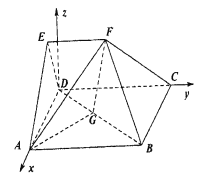
如图,过![]() 点作平面
点作平面![]() 的垂线
的垂线![]() ,
,
以点![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, 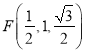 ,
, ![]() ,
, 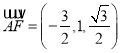
![]() ,.
,.
设![]() ,
, ![]() ,则
,则![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() ,
, ![]()
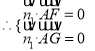 即
即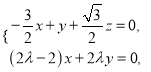 令
令![]() ,得
,得
![]() .
.
易知平面![]() 的一个法向量
的一个法向量![]() .
.
由已知得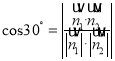
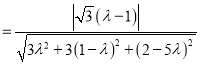
![]() ,
,
化简得![]() ,
, ![]() .
.
![]() 当点
当点![]() 满足
满足![]() 时,平面
时,平面![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了20名学生的答题数据进行统计,结果如表:

(Ⅰ)根据题中数据,估计中240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设![]() 为第
为第![]() 题的实测难度,请用
题的实测难度,请用![]() 和
和![]() 设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.