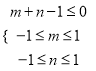题目内容
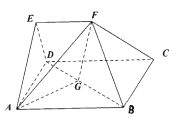
【题目】如图,已知正方体![]() 的棱长为1,点
的棱长为1,点![]() 是棱
是棱![]() 上的动点,
上的动点,![]() 是棱
是棱![]() 上一点,
上一点,![]() .
.

(1)求证:![]() ;
;
(2)若直线![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并证明你的结论;
的位置,并证明你的结论;
(3)设点![]() 在正方体的上底面
在正方体的上底面![]() 上运动,求总能使
上运动,求总能使![]() 与
与![]() 垂直的点
垂直的点![]() 所形成的轨迹的长度.(直接写出答案)
所形成的轨迹的长度.(直接写出答案)
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】分析:(1)要证![]() ,需证明
,需证明![]() 平面
平面![]() ,要证
,要证![]() ,
,![]() ,用综合法书写即可。
,用综合法书写即可。
(2)要证明![]() 平面
平面![]() ,需证明
,需证明![]() ,需证
,需证![]() 面
面![]() ,需证
,需证![]() 面
面![]() ,需证:
,需证:![]() ,要证明:
,要证明:![]() ,由此确定E点的位置。
,由此确定E点的位置。
(3)过![]() 三等分点作
三等分点作![]() 平行线,对于上面的任意一点
平行线,对于上面的任意一点![]() 都有
都有![]() ,再求长度。
,再求长度。
详解:(1)证明:连结![]() ,
,![]() 是正方形,所以
是正方形,所以![]() ,
,
在正方体![]() 中,
中,![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() .
.
(2)当![]() 时,直线
时,直线![]() 平面
平面![]() .
.
证明如下:
过点![]() 在平面
在平面![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
连结![]() ,交
,交![]() 于点
于点![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
在正方体![]() 中,
中,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() 面
面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以直线![]() 平面
平面![]() .
.
(3)![]() .
.

【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如表:
网购金额 (单位:千元) | 频数 | 频率 |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
合计 | 60 |
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为![]() .
.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%,现部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨:产生了20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
则这三天中恰有两天降雨的概率约为__________.