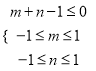题目内容
【题目】如图,已知点![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形,点
为底边的等腰三角形,点![]() 在直线
在直线![]() :
:![]() 上.
上.

(1)求![]() 边上的高
边上的高![]() 所在直线的方程;
所在直线的方程;
(2)求![]() 的面积.
的面积.
【答案】解:(Ⅰ)由题意可知,E为AB的中点,∴E(3,2),……………………1分
且![]() ,……………………………………………………1分,
,……………………………………………………1分,
∴CE:y-2=x-3,即x-y-1=0.………………………………2分
(Ⅱ)由![]() 得C(4,3),…………………………………1分
得C(4,3),…………………………………1分
∴|AC|=|BC|=2,AC⊥BC,…………………………………………1分
∴![]()
【解析】
试题分析:
(1)由题意,求得直线![]() 的斜率,从而得到
的斜率,从而得到![]() ,利用直线的点斜式方程,即可求解直线
,利用直线的点斜式方程,即可求解直线![]() 的方程;
的方程;
(2)由![]() ,求得
,求得![]() ,利用两点间的距离公式和三角形的面积公式,即可求得三角形的面积.
,利用两点间的距离公式和三角形的面积公式,即可求得三角形的面积.
试题解析:
(Ⅰ)由题意可知,![]() 为
为![]() 的中点,
的中点,![]()
∴![]() ,且
,且![]() ,
,
∴![]() 所在直线方程为
所在直线方程为![]() ,
,
即![]() .
.
(Ⅱ)由![]() 得
得![]()
∴![]()
∴![]() ,
,![]()
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目