题目内容
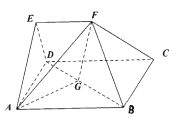
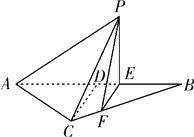
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
【答案】(1) VP-ACFE=![]() (2)
(2) ![]()
![]()
【解析】试题分析:(1)![]() ,S四边形ACFE=S△ABC-S△BEF=
,S四边形ACFE=S△ABC-S△BEF=![]() ,所以四棱锥P-ACFE的体积VP-ACFE=
,所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]() ;(2)V′(x)=0
;(2)V′(x)=0 ![]() ,所以
,所以![]()
![]() 。
。
试题解析:
(1)因为EF⊥AB,所以EF⊥PE.又因为PE⊥AE,EF∩AE=E,所以PE⊥平面ACFE. 因为EF⊥AB,CD⊥AB,且CD,EF共面,所以EF∥CD,
所以![]()
![]()
所以四边形ACFE的面积
S四边形ACFE=S△ABC-S△BEF=![]()
所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]()
(2)由(1)知. ![]() 令V′(x)=0
令V′(x)=0 ![]() 因为当
因为当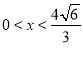 时,V′(x)>0, 当
时,V′(x)>0, 当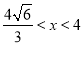 时,V′(x)<0.所以当
时,V′(x)<0.所以当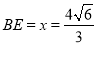 时,
时, 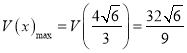

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目