题目内容
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)若过![]() 、
、![]() 、
、![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() :
: ![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(III)在(Ⅱ)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得以
使得以![]() 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出![]() 的取值范围,如果不存在,说明理由
的取值范围,如果不存在,说明理由
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)设![]() ,由
,由![]() ,所以
,所以![]() ,由于
,由于![]() ,即
,即![]() 为
为![]() 的中点,故
的中点,故![]() ,即
,即![]() ,于是
,于是![]() ,于是
,于是![]() 的外接圆圆心为
的外接圆圆心为![]() ,半径
,半径![]() ,该圆与直线
,该圆与直线![]() 相切,则
相切,则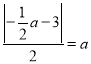 ,即可得出
,即可得出![]() 值,从而可求椭圆
值,从而可求椭圆![]() 的方程;
的方程;
(2)由(1)可知![]() ,设
,设![]() ,联立方程组
,联立方程组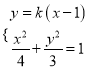 ,整理得
,整理得![]() ,写出韦达定理,由于菱形的对角线垂直,故
,写出韦达定理,由于菱形的对角线垂直,故![]() , 即
, 即![]() ,即
,即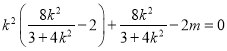 ,由已知条件知
,由已知条件知![]() 且
且![]() ,所以
,所以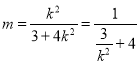 ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)设![]() ,由
,由![]() ,
,
知![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
由于![]() ,即
,即![]() 为
为![]() 的中点,
的中点,
故![]() ,所以
,所以![]() ,即
,即![]() ,
,
于是![]() ,于是
,于是![]() 的外接圆圆心为
的外接圆圆心为![]() ,半径
,半径![]() ,
,
该圆与直线![]() 相切,则
相切,则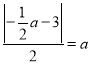 ,解得
,解得![]() ,
,
所以![]() ,所求椭圆的方程为
,所求椭圆的方程为![]() .
.
(2)由(1)可知![]() ,
,
设![]() ,联立方程组
,联立方程组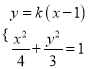 ,整理得
,整理得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
由于菱形的对角线垂直,故![]() ,
,
故![]() ,即
,即![]() ,
,
即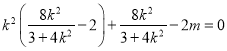 ,
,
由已知条件知![]() 且
且![]() ,
,
所以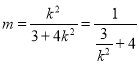 ,所以
,所以![]() ,
,
故存在满足题意的点![]() ,且
,且![]() 的取值范围是
的取值范围是![]() ,
,
当直线![]() 的斜率不存在时,不合题意.
的斜率不存在时,不合题意.

【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如表:
网购金额 (单位:千元) | 频数 | 频率 |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
合计 | 60 |
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为![]() .
.
(1)确定![]() ,
,![]() ,
,![]() ,
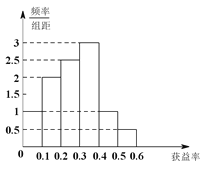
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.