题目内容
【题目】已知函数![]() (
(![]() >0,
>0, ![]() ≠1,
≠1, ![]() ≠﹣1),是定义在(﹣1,1)上的奇函数.
≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求实数![]() 的值;
的值;
(2)当![]() =1时,判断函数
=1时,判断函数![]() 在(﹣1,1)上的单调性,并给出证明;
在(﹣1,1)上的单调性,并给出证明;
(3)若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由函数![]() 是奇函数,
是奇函数, ![]() 对定义域内的所有自变量成立,可得
对定义域内的所有自变量成立,可得![]() 对定义域内的
对定义域内的![]() 都成立,可得
都成立,可得![]() ,从而可求出实数
,从而可求出实数![]() 的值;(2)先先根据单调性的定义判断并证明真数的单调性,分别两种情况讨论对数底数的范围,结合复合函数的单调性即可判断函数
的值;(2)先先根据单调性的定义判断并证明真数的单调性,分别两种情况讨论对数底数的范围,结合复合函数的单调性即可判断函数![]() 在
在![]() 上的单调性;(3)先根据
上的单调性;(3)先根据![]() 得到
得到![]() 的范围,再结合其为奇函数把
的范围,再结合其为奇函数把![]() 转化为
转化为![]() ,利用第二问的单调性即可求出实数
,利用第二问的单调性即可求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)∵函数![]() 是奇函数,∴
是奇函数,∴![]()
∴![]() ∴
∴![]() ;∴
;∴![]()
∴![]() ,
,
整理得![]() 对定义域内的
对定义域内的![]() 都成立.∴
都成立.∴![]() .
.
所以![]() 或
或![]() (舍去)∴
(舍去)∴![]() .
.
(2)由(1)可得![]() ;令
;令![]()
设![]() ,则
,则![]()
∵![]() ∴
∴![]() ,
,![]() ∴
∴![]() .
.
当![]() 时,
时,![]() ,即
,即![]() .
.
∴当![]() 时,
时, ![]() 在(﹣1,1)上是减函数.
在(﹣1,1)上是减函数.
当![]() 时,
时, ![]() ,即
,即![]() .
.
∴当![]() 时,
时, ![]() 在(﹣1,1)上是增函数.
在(﹣1,1)上是增函数.
(3)∵![]() , ∴
, ∴![]() ,
,
由![]() ,得
,得![]() ,
,
∵函数![]() 是奇函数, ∴
是奇函数, ∴![]() ,
,
故由(2)得![]()
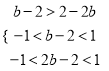
解得![]() ∴实数
∴实数![]() 的取值范围是
的取值范围是![]() 。
。

 阅读快车系列答案
阅读快车系列答案【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 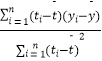 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?