题目内容
14.(1)已知关于方程x2+2(m-1)x-2m=0的两根都在[-2,2)内.则实数m的取值范围是什么?(2)关于x的方程2kx2-2x-3k-2=0的两实根一个小于1,另一个大于1,则实数k的取值范围是什么?
(3)方程x2-(a+4)x-2a2+5a+3=0的两根都在区间[-1,3]上,求实数m的取值范围.
(4)方程x2-2ax+4=0的两根均大于1,求实数a的取值范围.
分析 构造函数,结合函数的图象,建立不等式,即可得出结论.
解答 解:(1)设f(x)=x2+2(m-1)x-2m,则$\left\{\begin{array}{l}{△=4(m-1)^{2}+8m≥0}\\{-2≤1-m<2}\\{4-4(m-1)-2m≥0}\\{4+4(m-1)-2m>0}\end{array}\right.$,∴0$<m≤\frac{4}{3}$;
(2)因为方程有两实根,所以二次项系数不为0,则k≠0.
又因为方程2kx2-2x-3k-2=0的两实根,一个小于1,另一个大于1,则存在两种情况:
情况1:当k>0时,:函数f(x)=2kx2-2x-3k-2 图象开口向上,此时只需f(1)<0 即可.
即 2k-2-3k-2<0 解得 k>-4.结合前提条件有k>0.
情况2:当k<0时,函数2kx2-2x-3k-2 图象开口向下,此时只需f(1)>0,即可
即 2k-2-3k-2>0 解得 k<-4.结合前提条件有k<-4.
综上,满足题意的 k的取值范围是k<-4 或 k>0.
(3)令g(x)=x2-(a+4)x-2a2+5a+3,由x2-(a+4)x-2a2+5a+3=0的两根都在区间[-1,3],
可得$\left\{\begin{array}{l}{(a+4)^{2}+8{a}^{2}-20a-12≥0}\\{-1≤\frac{1}{2}(a+4)≤3}\\{1+a+4-2{a}^{2}+5a+3≥0}\\{9-3(a+4)-2{a}^{2}+5a+3≥0}\end{array}\right.$,由此求得0≤a≤1;
(4)要使两根均大于1,必须$\left\{\begin{array}{l}{4{a}^{2}-16≥0}\\{1-2a+4>0}\\{a>1}\end{array}\right.$,解得2≤a<$\frac{5}{2}$.
点评 此题主要考查的是方程根的分布问题,对于此类题目可以转化为求抛物线零点分布的问题,利用函数思想解答,对学生做题的灵活性要求较高.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | [1,+∞) | B. | $[-\frac{1}{2},1)$ | C. | $(-∞,-\frac{3}{2}]$ | D. | (0,+∞) |
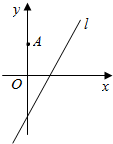 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.