题目内容
9.已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x,若对于任意的x∈[a,a+2],均有f(x+a)≥f2(x),则实数a取值范围是( )| A. | [1,+∞) | B. | $[-\frac{1}{2},1)$ | C. | $(-∞,-\frac{3}{2}]$ | D. | (0,+∞) |
分析 根据函数为偶函数,求出函数f(x)的表达式,然后将不等式f(x+a)≥f2(x)化简,对a进行讨论,将x解出来,做到参数分离,由恒成立思想,即可求出a的范围.
解答 解:由题意,f(x)=$\left\{\begin{array}{l}{{2}^{x},x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$
(1)当a≥0时,即有2x+a≥22x,x≤a,不合
(2)当a+2≤0时,即有$(\frac{1}{2})^{x+a}$≥$(\frac{1}{2})^{2x}$,x≥a,恒成立,a≤-2符合
(3)当-2<a<0时,若x+a>0,则a+2≥-a,a≥-1由(1)得不合
若x<0由(2)得成立,则x+a<0,x>0时恒成立,即$(\frac{1}{2})^{x+a}$≥22x,x≤-$\frac{a}{3}$,
∴a+2≤-$\frac{a}{3}$,∴a$≤-\frac{3}{2}$,∴-2<a≤-$\frac{3}{2}$
综上,实数a的取值范围a≤-$\frac{3}{2}$
故选:C.
点评 本题主要考查函数的奇偶性及运用,求出函数在定义域上的解析式是解题的关键,考查解决恒成立问题的常用方法:参数分离,必须掌握.

练习册系列答案
相关题目
1.过点A(-2,3)作直线与抛物线y2=8x在第一象限相切于点B,记抛物线的焦点为F,则直线BF的斜率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
18.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,则f(f(x))≤3的解集为( )
| A. | (-∞,-3] | B. | [-3,+∞) | C. | (-∞,$\sqrt{3}$] | D. | [$\sqrt{3}$,+∞) |
19.设集合A={x|-1<x<4},B={-1,1,2,4},则A∩B=( )
| A. | {1,2} | B. | {-1,4} | C. | {-1,2} | D. | {2,4} |
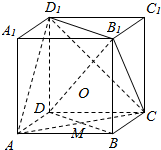 如图所示,在正方体ABCD-A1B1C1D1中,B1D与平面ACD1交于点O,BD与平面ACD1交于点M,求证:M,O,D1三点共线.
如图所示,在正方体ABCD-A1B1C1D1中,B1D与平面ACD1交于点O,BD与平面ACD1交于点M,求证:M,O,D1三点共线.