题目内容
【题目】选修4-4:坐标系与参数方程
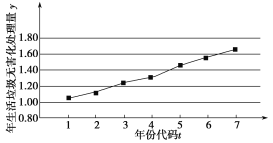
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)若![]() 是直线
是直线![]() 与圆面
与圆面![]() 的公共点,求
的公共点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)利用极坐标与直角坐标的互化公式,即可求解圆![]() 的普通方程;
的普通方程;
(Ⅱ)解法一:设![]() ,将直线
,将直线![]() 的参数方程代入
的参数方程代入![]() ,得
,得![]() ,又由直线
,又由直线![]() 过
过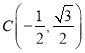 ,圆
,圆![]() 的半径是
的半径是![]() ,即求解
,即求解![]() 的范围,进而得到
的范围,进而得到![]() 的取值范围;
的取值范围;
解法二:求得直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 的坐标,由点
的坐标,由点![]() 在线段
在线段![]() 上,得
上,得![]() 的最大值和最小值,即可得到
的最大值和最小值,即可得到![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)∵圆![]() 的极坐标方程为
的极坐标方程为
![]()
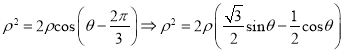
又![]() ,
,
![]() ∴圆
∴圆![]() 的普通方程为
的普通方程为![]()
(Ⅱ)解法一:设![]() ,圆
,圆![]() 的方程
的方程![]() 即
即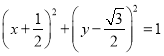 ,
,
∴圆![]() 的圆心是
的圆心是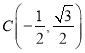 ,半径
,半径![]()
将直线![]() 的参数方程
的参数方程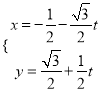 (
(![]() 为参数)代入
为参数)代入![]() ,得
,得![]()
又∵直线![]() 过
过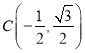 ,圆
,圆![]() 的半径是1,
的半径是1,
![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
解法二:圆![]() 的方程
的方程![]() 即
即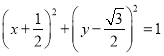 ,
,
将直线![]() 的参数方程
的参数方程 (
(![]() 为参数)化为普通方程:
为参数)化为普通方程: ![]()
∴直线![]() 与圆
与圆![]() 的交点为
的交点为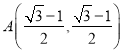 和
和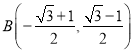 ,故点
,故点![]() 在线段
在线段![]() 上
上
从而当![]() 与点
与点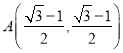 重合时,
重合时, ![]() ;
;
当![]() 与点
与点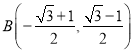 重合时,
重合时, ![]() .
.

练习册系列答案
相关题目