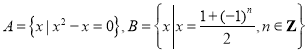题目内容
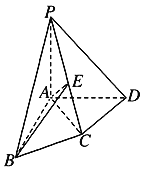
【题目】在
中，
且
，
边上的中线长为
，则的面积是____．
【答案】
【解析】
根据题意，将
变形可得sinB=1+cosC，又由B+C=
，则sinB=1+cosC可以变形为cos（C+
）=﹣1，分析可得C的值，进而可得B的值，分析可得，△ABC为等腰三角形，设D为BC中点，AD=
，设AC=x，在△ACD中，由余弦定理可得cosC=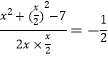
，计算可得x的值，由三角形面积公式计算可得答案．
根据题意，△ABC中，，则有
sinB=
，变形可得sinB=1+cosC，
则有cocC=sinB﹣1＜0，则C为钝角，B为锐角；
又由A=
，则B+C=，
则sinB=1+cosCsin（﹣C）=1+cosCcos（C+）=﹣1，
C为钝角，则C=
，B=﹣C=，
则△ABC中，A=B=，则有AC=BC，△ABC为等腰三角形，
设D为BC中点，AD=，设AC=x，
则有cosC=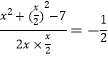
解可得x=2，
则S△ABC=×AC×BC×sinC=×2×2×sin=
故答案为:
【题目】近年来，某市为了促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的分类垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾，数据统计如下(单位：吨)：
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率P；
(2)试估计生活垃圾投放错误的概率；
(3)假设厨余垃圾在“厨余垃圾”箱，“可回收物”箱，“其他垃圾”箱的投放量分别为a、b、c，其中a＞0，a＋b＋c＝600. 当数据a、b、c的方差s2最大时，写出a、b、c的值(结论不要求证明)，并求出此时s2的值．
【题目】针对某地区的一种传染病与饮用水进行抽样调查发现:饮用干净水得病5人，不得病50人；饮用不干净水得病9人，不得病22人。
（1）作出2×2列联表
（2）能否有90％的把握认为该地区中得传染病与饮用水有关?
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
