题目内容
15.在区间[1,4]和[2,4]内分别取一个数记为a,b,则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆的概率为$\frac{1}{3}$.分析 本题考查的知识点是几何概型的意义,关键是要找出方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆时(a,b)点对应的平面图形的面积大小和区间[1,4]和[2,4]分别各取一个数(a,b)点对应的平面图形的面积大小,并将他们一齐代入几何概型计算公式进行求解.
解答 解:若方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆,则a>b
它对应的平面区域如下图中阴影部分所示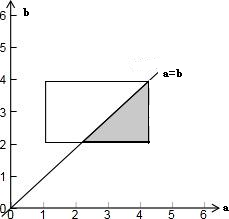
则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆的概率P=$\frac{{S}_{阴影}}{{S}_{矩形}}$=$\frac{\frac{1}{2}×2×2}{3×2}=\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题考查了几何概型公式的运用;
几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式解答.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3.某市对汽车限购政策进行了调查,在参加调查的300名有车人中116名持反对意见,200名无车人中有121名持反对意见,在运用这些数据说明“拥有车辆”与“反对汽车限购政策”是否有关系时,最有说服力的方法是( )
| A. | 平均数与方差 | B. | 回归直线方程 | C. | 独立性检验 | D. | 概率 |
10.函数y=$\frac{1}{{\sqrt{1-{{log}_3}({{2^x}-1})}}}$的定义域为( )
| A. | [0,2) | B. | (0,2] | C. | (0,2) | D. | (0,+∞) |
20.已知M=$\int_0^1{\frac{1}{x+1}dx,N=\int_0^{\frac{π}{2}}{cosxdx}}$,由图示程序框图输出的S为( )
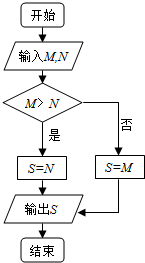

| A. | 1 | B. | ln2 | C. | $\frac{π}{2}$ | D. | 0 |
7.若复数z满足iz=2+4i,则z在复平面内对应的点的坐标是( )
| A. | (4,2) | B. | (2,-4) | C. | (2,4) | D. | (4,-2) |