题目内容
20．已知M=$\int_0^1{\frac{1}{x+1}dx，N=\int_0^{\frac{π}{2}}{cosxdx}}$，由图示程序框图输出的S为（ ）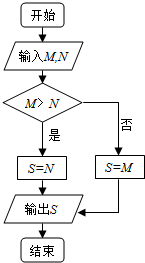
| A． | 1 | B． | ln2 | C． | $\frac{π}{2}$ | D． | 0 |
分析 根据积分的定义，分别解出M和N，再判断M与N的大小，代入程序图进行求解．
解答 解：∵M=${∫}_{0}^{1}$$\frac{1}{x+1}$dx=ln（x+1）|${\;}_{0}^{1}$=ln2，N=${∫}_{0}^{\frac{π}{2}}$cosxdx=sinx|${\;}_{0}^{\frac{π}{2}}$=1，
∴ln2＜1
∴M＜N，
由程序图可知求两个数的最大值，输出的是最小的一个数，
∴S=ln2，
故选：B．
点评 本题考查了定积分的计算和程序框图，属于基础题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10．在△ABC内部随机取一点P，则事件“△PBC”的面积不大于△ABC面积的$\frac{1}{4}$”的概率是（ ）
| A． | $\frac{7}{16}$ | B． | $\frac{9}{16}$ | C． | $\frac{5}{9}$ | D． | $\frac{4}{9}$ |
如图，在四棱锥P-ABCD中，AB∥CD，PA⊥AD，CD⊥AD，PA=AD=CD=2AB，E，F分别为PC，CD的中点，DE=EC．
12．M为抛物线y2=8x上一点，F为抛物线的焦点，∠MFO=120°（O为坐标原点），N（-2，0），则直线MN的斜率为（ ）
| A． | $±\frac{1}{3}$ | B． | ±$\frac{1}{2}$ | C． | ±$\frac{\sqrt{3}}{2}$ | D． | ±$\frac{\sqrt{2}}{2}$ |
9．已知点A（-1，1），B（1，2），C（-2，-1），D（3，4），则向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为（ ）
| A． | $-\frac{{3\sqrt{15}}}{2}$ | B． | $\frac{{3\sqrt{15}}}{2}$ | C． | $-\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{3\sqrt{2}}}{2}$ |