题目内容
6.在平面直角坐标系xOy中,已知A为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1上的动点,MN为圆(x-1)2+y2=1的一条直径,则|$\overrightarrow{AM}$•$\overrightarrow{AN}$|的最大值为15.分析 由题意画出图形,得到椭圆上离圆心最远的点A,在设出圆的直径两端点的坐标,由平面向量数量积运算求得答案.
解答 解:如图,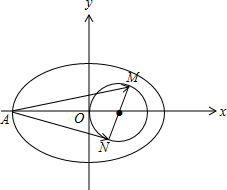
圆(x-1)2+y2=1在椭圆内,椭圆上的所有点只有左顶点到圆心(1,0)距离最远,
由题意可设圆的直径的两个端点为M(1+cosθ,sinθ),N(1-cosθ,-sinθ),
又A(-3,0),
∴$\overrightarrow{AM}=(4+cosθ,sinθ),\overrightarrow{AN}=(4-cosθ,-sinθ)$,
则$\overrightarrow{AM}$•$\overrightarrow{AN}$=16-cos2θ-sin2θ=15.
∴|$\overrightarrow{AM}$•$\overrightarrow{AN}$|的最大值为15.
故答案为:15.
点评 本题考查椭圆的简单性质,考查了平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
14.已知复数z满足z2=2i,则z=( )
| A. | 1+i | B. | 1-i | C. | ±(1-i) | D. | ±(1+i) |
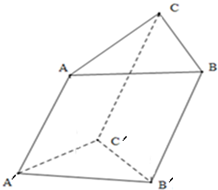 斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.
斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.