题目内容
7.若复数z满足iz=2+4i,则z在复平面内对应的点的坐标是( )| A. | (4,2) | B. | (2,-4) | C. | (2,4) | D. | (4,-2) |
分析 把已知的等式变形,利用复数代数形式的乘除运算化简得答案.
解答 解:由iz=2+4i,
得$z=\frac{2+4i}{i}=\frac{-i(2+4i)}{-i•i}=4-2i$.
∴则z在复平面内对应的点的坐标是:(4,-2).
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
2.执行如图的程序框图,如果输入a=4,那么输出的n的值为( )
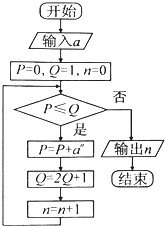

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
12.M为抛物线y2=8x上一点,F为抛物线的焦点,∠MFO=120°(O为坐标原点),N(-2,0),则直线MN的斜率为( )
| A. | $±\frac{1}{3}$ | B. | ±$\frac{1}{2}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
19.设a=logπ3,b=log3π,c=lnπ,则( )
| A. | c>a>b | B. | b>c>a | C. | c>b>a | D. | b>a>c |
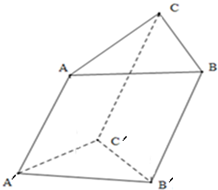 斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.
斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.