题目内容

5．已知命题P为：“?x∈R，|x|≤0”，则￢P为：?x∈R，|x|＞0．

分析 直接利用特称命题的否定是全称命题写出结果即可．

解答 解：因为特称命题的否定是全称命题，所以，命题P为：“?x∈R，|x|≤0”，则￢P为：?x∈R，|x|＞0．
故答案为：?x∈R，|x|＞0．

点评 本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．

练习册系列答案
相关题目
15．在同一坐标系中，将椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1变换成单位圆的伸缩变换是（　　）
A．φ：$\left\{\begin{array}{l}{x′=5x}\\{{y}^{′}=4y}\end{array}\right.$B．φ：$\left\{\begin{array}{l}{{x}^{′}=4x}\\{{y}^{′}=5y}\end{array}\right.$
C．φ：$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{4}x}\\{{y}^{′}=\frac{1}{5}y}\end{array}\right.$D．φ：$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{5}x}\\{{y}^{′}=\frac{1}{4}y}\end{array}\right.$
16．下列四个命题中，真命题的个数是②③
①若b2=ac，则a、b、c成等比数列；
②若{an}为等差数列，且常数c＞0，则数列{c${\;}^{{a}_{n}}$}为等比数列．
③若{an}为等比数列，则数列{|an|}为等比数列；
④常数列既是等比数列，又是等差数列．
13．已知函数f（x）=x2-ax+1，其中a∈R，且a≠0．
（1）若f（x）在[-1，1]上不是单调函数，求a的取值范围；
（2）求y=|f（x）|在区间[0，|a|]上的最大值．
20．已知函数f（x）=ln（1+ax）-ax，（其中a为实数，且a≠0）．
（1）求函数f（x）的单调区间；
（2）关于x方程f（x）-a=0在[-1，1]上是否有两个不等实根？若有，求实数a的取值范围；若没有，请说明理由；
（3）若数列{an}满足：a1=1，an+1=（1+$\frac{1}{{n}^{2}+n}$）an+$\frac{1}{{2}^{n}}$，n∈N*，证明：对于任意的正整数n，都有an＜e2，其中无理数e=2.71828．
10．在△ABC内部随机取一点P，则事件“△PBC”的面积不大于△ABC面积的$\frac{1}{4}$”的概率是（　　）
A．$\frac{7}{16}$B．$\frac{9}{16}$C．$\frac{5}{9}$D．$\frac{4}{9}$
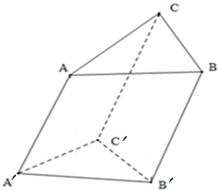17．斜三棱柱底面边长是4cm的正三角形，．侧棱长3cm，侧棱∠AA′C′=∠AA′B′=60°．
（1）求证：C′B′⊥AA′；
（2）求三棱柱的侧面积；
（3）求三棱柱的体积．
（提示：过点A作底面A′B′C′的垂线，垂足为P．则点P在∠C′A′B′的角平分线上）
14．已知复数z满足z2=2i，则z=（　　）
A．1+iB．1-iC．±（1-i）D．±（1+i）
15．在区间[1，4]和[2，4]内分别取一个数记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆的概率为$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网