题目内容

10．函数y=$\frac{1}{{\sqrt{1-{{log}_3}（{{2^x}-1}）}}}$的定义域为（　　）
A．[0，2）B．（0，2]C．（0，2）D．（0，+∞）

分析 根据对数函数的性质得到不等式，解出即可．

解答 解：由题意得：
1-${log}_{3}^{{（2}^{x}-1）}$＞0，
∴${log}_{3}^{{（2}^{x}-1）}$＜1，
∴0＜2x-1＜3，
∴0＜x＜2，
故选：C．

点评 本题考察了函数的定义域，考察对数函数的性质问题，是一道基础题．

练习册系列答案
相关题目
20．已知函数f（x）=ln（1+ax）-ax，（其中a为实数，且a≠0）．
（1）求函数f（x）的单调区间；
（2）关于x方程f（x）-a=0在[-1，1]上是否有两个不等实根？若有，求实数a的取值范围；若没有，请说明理由；
（3）若数列{an}满足：a1=1，an+1=（1+$\frac{1}{{n}^{2}+n}$）an+$\frac{1}{{2}^{n}}$，n∈N*，证明：对于任意的正整数n，都有an＜e2，其中无理数e=2.71828．
1．已知数列{an}的首项a1=1，an+1=$\frac{4{a}_{n}}{{a}_{n}+2}$，n∈N*．
（1）证明：数列{$\frac{1}{{a}_{n}}$-$\frac{1}{2}$}是等比数列；
（2）求数列{$\frac{2n}{{a}_{n}}$}的前n项和Sn．
18．现有4个学生去参加某高校的面试，面试要求用汉语或英语中的一种回答问题，每个学生被要求用英语回答问题的概率均为$\frac{1}{3}$．
（Ⅰ）求这4个学生中恰有2人用英语回答问题的概率；
（Ⅱ）若m，n分别表示用汉语，英语回答问题的人数，记X=|m-n|，求随机变量X的概率分布和数学期望E（X）．
5．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上为减函数，若$f（{ln\frac{n}{m}}）$+$f（{ln\frac{m}{n}}）$-2f（1）＞0，则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是（　　）
A．（e，+∞）B．[2，e）C．$（{e+\frac{1}{e}，+∞}）$D．$[{2，e+\frac{1}{e}}）$
15．在区间[1，4]和[2，4]内分别取一个数记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示焦点在x轴上的椭圆的概率为$\frac{1}{3}$．
2．执行如图的程序框图，如果输入a=4，那么输出的n的值为（　　）
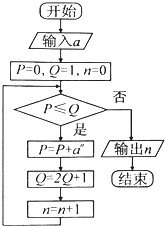
A．5B．4C．3D．2
19．设a=logπ3，b=log3π，c=lnπ，则（　　）
A．c＞a＞bB．b＞c＞aC．c＞b＞aD．b＞a＞c
20．某厂生产甲、乙、丙三种零件，每种零件均有A、B两种型号，某月的产量如下表（单位：个）：
甲乙丙
A100150m
B300450600
用分层抽样的方法在这个月生产的零件中抽取50件，其中有甲种零件10件．
（Ⅰ） 求m的值；
（Ⅱ） 用分层抽样的方法在丙种零件中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2个，求至少有1个A型零件的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网