题目内容
(
(本小题满分12分)
已知数列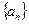 中,
中,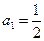 ,且当
,且当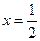 时,函数
时,函数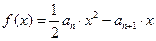 取得极值。
取得极值。
(Ⅰ)求数列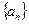 的通项公式;
的通项公式;
(Ⅱ)数列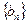 满足:
满足: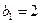 ,
,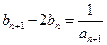 ,证明:
,证明: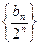 是等差数列,并求数列
是等差数列,并求数列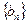 的通项公式通
的通项公式通 项及前
项及前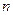 项和
项和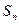 .
.
(本小题满分12分)
已知数列
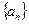 中,
中,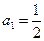 ,且当
,且当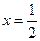 时,函数
时,函数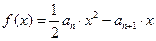 取得极值。
取得极值。(Ⅰ)求数列
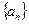 的通项公式;
的通项公式;(Ⅱ)数列
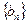 满足:
满足: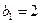 ,
,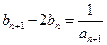 ,证明:
,证明: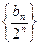 是等差数列,并求数列
是等差数列,并求数列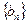 的通项公式通
的通项公式通 项及前
项及前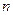 项和
项和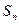 .
.(1)
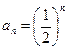
(2)
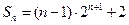
解:(Ⅰ)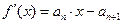
 ……1分
……1分
由题意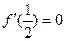 得
得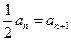 ……3分
……3分
∴数列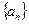 是首项为,公比为的等比数列,∴
是首项为,公比为的等比数列,∴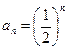 …………5分
…………5分
(Ⅱ)由(1)知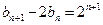 ,∴
,∴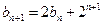
∴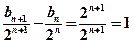
∴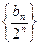 是以1为首项,1位公差的等差数列 …………7分
是以1为首项,1位公差的等差数列 …………7分
∴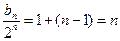 ,∴
,∴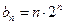 ……………8分
……………8分
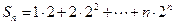
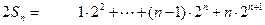
两式相减得: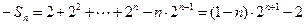 ………11分
………11分
∴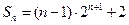
 …………12分
…………12分
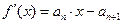
 ……1分
……1分 由题意
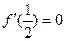 得
得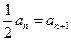 ……3分
……3分∴数列
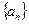 是首项为,公比为的等比数列,∴
是首项为,公比为的等比数列,∴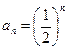 …………5分
…………5分(Ⅱ)由(1)知
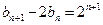 ,∴
,∴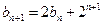
∴
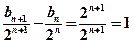
∴
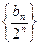 是以1为首项,1位公差的等差数列 …………7分
是以1为首项,1位公差的等差数列 …………7分∴
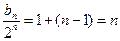 ,∴
,∴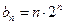 ……………8分
……………8分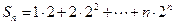
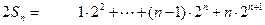
两式相减得:
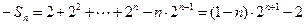 ………11分
………11分∴
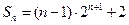
 …………12分
…………12分
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

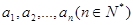 满足条件:
满足条件: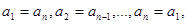
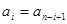 ,
,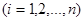 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列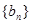 是项数不超过
是项数不超过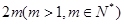 的“对称数列”,并使得
的“对称数列”,并使得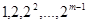 依次为该数列中连续的前
依次为该数列中连续的前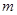 项,则数列
项,则数列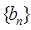 的前2009项和
的前2009项和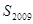 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )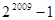 ②
②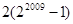 ③
③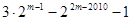 ④
④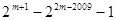
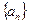 中,
中, ,且当
,且当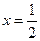 时,函数
时,函数
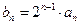 ,证明数列
,证明数列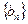 为等差数列;
为等差数列;
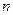 项和为
项和为 ,求
,求 
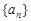 是等差数列,且
是等差数列,且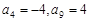 ,
,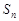 是数列
是数列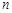 项和,则( )
项和,则( )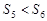
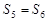
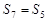
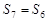
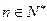 ,总有
,总有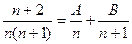 成立,求常数
成立,求常数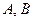 的值;
的值;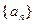 中,
中, ,
,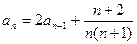 (
(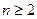 ,
,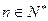 ),求通项
),求通项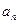 ;
;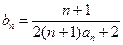 ,从数列
,从数列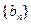 中依次取出第
中依次取出第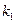 项,第
项,第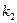 项,…第
项,…第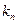 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列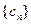 ,其中
,其中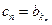 ,其中
,其中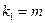 ,
,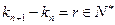 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 }的前5项和
}的前5项和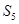 ="25," 且
="25," 且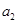 ="3," 则
="3," 则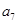 = ( )
= ( )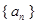 的前
的前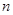 项和为
项和为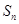 ,且
,且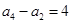 ,
,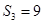 ,则数列
,则数列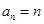
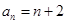
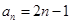
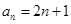
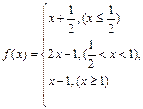 若数列
若数列 满足
满足 =
=