题目内容
(本小题满分13分)
已知△ABC中,角A、B、C成等差数列,求证:+=
已知△ABC中,角A、B、C成等差数列,求证:+=

【证法一】因为△ABC中,角A、B、C成等差数列,

所以B=600,… …………………2分
…………………2分
由余弦定理b2= c2+a2-2cacosB………………4分
即b2= c2+a2-ca
所以c2+a2=ac+b2………………6分
所以c(b+c)+a(a+b)=" (a+b)" (b+c) ………………9分
所以+=3………………12分
因此 +=.……………………13分
【证法二】 要证 +=
需证: +=3
即证:c(b+c) +a(a+b)=" (a+b)" (b+c)
+a(a+b)=" (a+b)" (b+c)
即证:c2+a2=ac+b2
因为△ABC中,角A、B、C成等差数列,
所以B=600,由余弦定理b2= c2+a2-2cacosB
即b2= c2+a2-ca 所以c2+a2=ac+b2
因此 +=.

所以B=600,…
 …………………2分
…………………2分由余弦定理b2= c2+a2-2cacosB………………4分
即b2= c2+a2-ca
所以c2+a2=ac+b2………………6分
所以c(b+c)+a(a+b)=" (a+b)" (b+c) ………………9分
所以+=3………………12分
因此 +=.……………………13分
【证法二】 要证 +=
需证: +=3
即证:c(b+c)
 +a(a+b)=" (a+b)" (b+c)
+a(a+b)=" (a+b)" (b+c)即证:c2+a2=ac+b2
因为△ABC中,角A、B、C成等差数列,
所以B=600,由余弦定理b2= c2+a2-2cacosB
即b2= c2+a2-ca 所以c2+a2=ac+b2
因此 +=.
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数. 满足
满足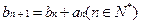 ,
, ,求数列
,求数列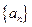 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,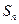 为
为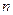 项和.
项和.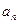 及
及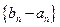 是首项为1,公比为3的等
是首项为1,公比为3的等 比数列,求数列
比数列,求数列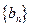 的通项公式及其前
的通项公式及其前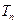 .
.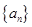 的前
的前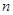 项和为
项和为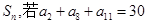 ,那么
,那么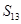 值的是( )
值的是( ) 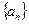 中,
中,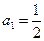 ,且当
,且当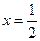 时,函数
时,函数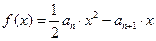 取得极值。
取得极值。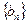 满足:
满足: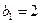 ,
,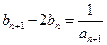 ,证明:
,证明: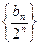 是等差数列,并求数列
是等差数列,并求数列 项及前
项及前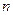 项和
项和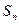 .
.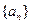 中,已知
中,已知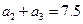 ,
,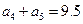 ,则等差数列
,则等差数列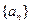 的前n项的乘积
的前n项的乘积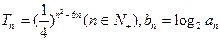 ,则数列
,则数列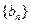 的前n项和
的前n项和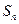 中的最大值是 ( )
中的最大值是 ( )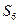
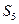
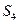
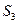
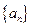 中,
中, ,则此数列的前
,则此数列的前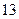 项的和等于___________.
项的和等于___________.