题目内容
如果有穷数列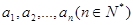 满足条件:
满足条件: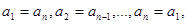
即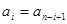 ,
,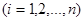 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列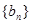 是项数不超过
是项数不超过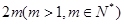 的“对称数列”,并使得
的“对称数列”,并使得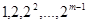 依次为该数列中连续的前
依次为该数列中连续的前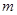 项,则数列
项,则数列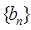 的前2009项和
的前2009项和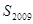 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )
①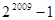 ②
②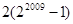 ③
③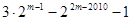 ④
④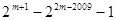
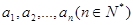 满足条件:
满足条件: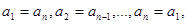
即
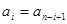 ,
,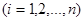 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列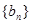 是项数不超过
是项数不超过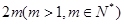 的“对称数列”,并使得
的“对称数列”,并使得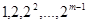 依次为该数列中连续的前
依次为该数列中连续的前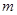 项,则数列
项,则数列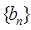 的前2009项和
的前2009项和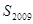 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )①
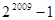 ②
②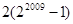 ③
③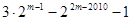 ④
④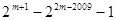
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
D
由于新定义了对称数列,且已知数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,故数列{bn}的前2009项和需分情况讨论,然后利用等比数列的前n项和定义直接可求得,从而判断①②的正确与否;对于③④,先从等比数列的求和公式求出任意2m项的和,在利用减法得到需要的前2009项的和,即可判断.
解:因为数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,
所以分数列的项数是偶数和奇数讨论.
若数列含偶数项,则数列可设为1,21,22,…,2m-1,2m-1,…,22,21,1
当m-1≥2008时,S2009=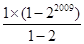 =22009-1,所以①正确;
=22009-1,所以①正确;
当1004≤m-1<2008时,S2009=2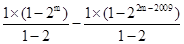 =2m+1-22m-2009-1,所以④正确;
=2m+1-22m-2009-1,所以④正确;
若数列含奇数项,则数列可设为可设为1,21,22,…,2m-2,2m-1,2m-2…,22,21,1
当m-1≥2008时,S2009=22009-1;
当1004≤m-1<2008时,所以S2009=2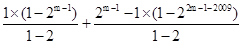 =3?2m-1-22m-2010-1,所以③正确.
=3?2m-1-22m-2010-1,所以③正确.
故选D.
解:因为数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,
所以分数列的项数是偶数和奇数讨论.
若数列含偶数项,则数列可设为1,21,22,…,2m-1,2m-1,…,22,21,1
当m-1≥2008时,S2009=
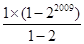 =22009-1,所以①正确;
=22009-1,所以①正确;当1004≤m-1<2008时,S2009=2
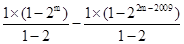 =2m+1-22m-2009-1,所以④正确;
=2m+1-22m-2009-1,所以④正确;若数列含奇数项,则数列可设为可设为1,21,22,…,2m-2,2m-1,2m-2…,22,21,1
当m-1≥2008时,S2009=22009-1;
当1004≤m-1<2008时,所以S2009=2
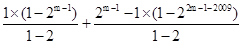 =3?2m-1-22m-2010-1,所以③正确.
=3?2m-1-22m-2010-1,所以③正确.故选D.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数. 满足
满足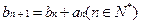 ,
, ,求数列
,求数列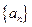 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,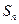 为
为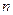 项和.
项和.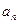 及
及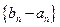 是首项为1,公比为3的等
是首项为1,公比为3的等 比数列,求数列
比数列,求数列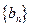 的通项公式及其前
的通项公式及其前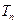 .
.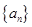 的前
的前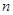 项和为
项和为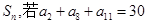 ,那么
,那么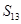 值的是( )
值的是( ) 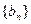 满足:
满足: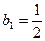 ,
,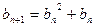 ,
, 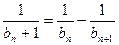 ;
;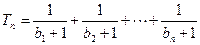 ,对任意的正整数
,对任意的正整数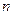 ,
,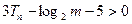 恒成立.求m的取值范围.
恒成立.求m的取值范围.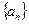 中,
中,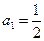 ,且当
,且当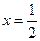 时,函数
时,函数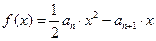 取得极值。
取得极值。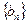 满足:
满足: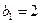 ,
,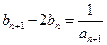 ,证明:
,证明: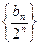 是等差数列,并求数列
是等差数列,并求数列 项及前
项及前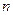 项和
项和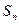 .
.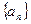 中,
中,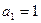 ,前10项和
,前10项和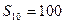 .
.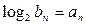 ,证明
,证明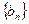 为等比数列,并求
为等比数列,并求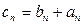 ,求
,求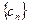 的前五项之和。
的前五项之和。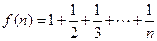 ,计算得
,计算得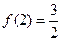 ,
,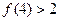 ,
,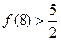 ,
,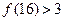 ,观察上述结果,可推测一般的结论为
,观察上述结果,可推测一般的结论为 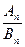 =
=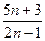 ,则
,则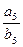 =
=