题目内容
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
【答案】
(1)解:∵S2=4,an+1=2Sn+1,n∈N*.
∴a1+a2=4,a2=2S1+1=2a1+1,
解得a1=1,a2=3,
当n≥2时,an+1=2Sn+1,an=2Sn﹣1+1,
两式相减得an+1﹣an=2(Sn﹣Sn﹣1)=2an,
即an+1=3an,当n=1时,a1=1,a2=3,
满足an+1=3an,
∴ ![]() =3,则数列{an}是公比q=3的等比数列,
=3,则数列{an}是公比q=3的等比数列,
则通项公式an=3n﹣1.
(2)解:an﹣n﹣2=3n﹣1﹣n﹣2,
设bn=|an﹣n﹣2|=|3n﹣1﹣n﹣2|,
则b1=|30﹣1﹣2|=2,b2=|3﹣2﹣2|=1,
当n≥3时,3n﹣1﹣n﹣2>0,
则bn=|an﹣n﹣2|=3n﹣1﹣n﹣2,
此时数列{|an﹣n﹣2|}的前n项和Tn=3+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
则Tn= 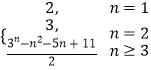 =
= 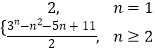 .
.
【解析】(1)根据条件建立方程组关系,求出首项,利用数列的递推关系证明数列{an}是公比q=3的等比数列,即可求通项公式an;(2)讨论n的取值,利用分组法将数列转化为等比数列和等差数列即可求数列{|an﹣n﹣2|}的前n项和.

练习册系列答案
相关题目