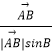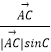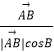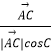题目内容
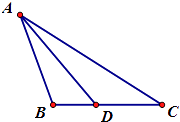
【题目】在△ABC中，已知B=45°，D是BC上一点，AD=5，AC=7，DC=3，求AB的长．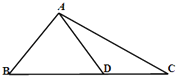 
【答案】解：法一：在△ADC中，由余弦定理得： 
∵∠ADC∈（0，π），∴∠ADC=120°，
∴∠ADB=180°﹣∠ADC=60°
在△ABD中，由正弦定理得： 
法二：在△ADC中，由余弦定理得 
∵∠ACD∈（0，π），∴ 
在△ABC中，由正弦定理得：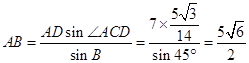 
故答案为： 
【解析】法一：先在△ADC中用余弦定理求出∠ADC的余弦值，进而求出∠ADC，再根据互补求出∠ADB，然后在△ABD中用正弦定理就可求出AB的长； 法二：先在△ADC中用余弦定理求出∠ACD的余弦值，在根据同角三角函数关系求出∠ACD的正弦，然后在△ABC中用正弦定理就可求出AB的长．
练习册系列答案
相关题目
【题目】为了考查培育的某种植物的生长情况，从试验田中随机抽取100柱该植物进行检测，得到该植物高度的频数分布表如下：
组序 | 高度区间 | 频数 | 频率 |
1 | [230，235） | 14 | 0.14 |
2 | [235，240） | ① | 0.26 |
3 | [240，245） | ② | 0.20 |
4 | [245，250） | 30 | ③ |
5 | [250，255） | 10 | ④ |
合计 | 100 | 1.00 | |
（Ⅰ）写出表中①②③④处的数据；
（Ⅱ）用分层抽样法从第3、4、5组中抽取一个容量为6的样本，则各组应分别抽取多少个个体？
（Ⅲ）在（Ⅱ）的前提下，从抽出的容量为6的样本中随机选取两个个体进行进一步分析，求这两个个体中至少有一个来自第3组的概率．
