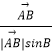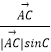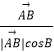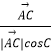题目内容
【题目】下列命题中真命题为( )
A.过点P(x0 , y0)的直线都可表示为y﹣y0=k(x﹣x0)
B.过两点(x1 , y1),(x2 , y2)的直线都可表示为(x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1)
C.过点(0,b)的所有直线都可表示为y=kx+b
D.不过原点的所有直线都可表示为 ![]()
【答案】B
【解析】解:当直线不过原点且直线和x轴垂直时,直线的斜率k不存在,如直线 x=3 等, 选项A、C、D不正确,
过两点(x1 , y1),(x2 , y2)的直线,当直线斜率存在且不等于0时,方程为 ![]() ,
,
即 (x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1).
当直线斜率不存在时,x1=x2 , 方程为 x=x1 , 可以写成(x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1)的形式.
当直线斜率等于0时,y1=y2 , 方程为 y=y1 , 可以写成(x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1)的形式.
综上,只有选项B正确,故选 B.
【考点精析】解答此题的关键在于理解两点式方程的相关知识,掌握直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2.
则:y-y1/y-y2=x-x1/x-x2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目