题目内容
【题目】设函数f（x）=sin（2x+ 
）+ 
cos（2x+ ），则（ ）
A.y=f（x）在（0， 
）单调递增，其图象关于直线x= 对称
B.y=f（x）在（0， ）单调递增，其图象关于直线x= 对称
C.y=f（x）在（0， ）单调递减，其图象关于直线x= 对称
D.y=f（x）在（0， ）单调递减，其图象关于直线x= 对称
【答案】D
【解析】解：函数f（x）=sin（2x+ 
）+ 
cos（2x+ ）， 化简可得：f（x）=sin（2x+ + 
）=cos2x．
根据余弦函数的图象和性质，2kπ≤2x≤2kπ+π，
可得： 
∴递减区间为[kπ， 
]，k∈Z．
∵对称轴方程2x=kπ，k∈Z．
∴函数的对称轴方程为x= 
，k∈Z．
故选D
利用辅助角公式基本公式将函数化为y=Asin（ωx+φ）的形式，将内层函数看作整体，放到正弦函数的增减区间上，解不等式得函数的单调区间；根据对称轴方程求解对称即可．
练习册系列答案
相关题目
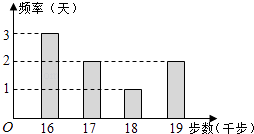
【题目】小王为了锻炼身体，每天坚持“健步走”，并用计步器进行统计．小王最近8天“健步走”步数的频数分布直方图（图1）及相应的消耗能量数据表（表1）如下：
健步走步数（前步） | 16 | 17 | 18 | 19 |
消耗能量（卡路里） | 400 | 440 | 480 | 520 |
（Ⅰ）求小王这8天“健步走”步数的平均数；
（Ⅱ）从步数为17千步，18千步，19千步的几天中任选2天，求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率．
