题目内容
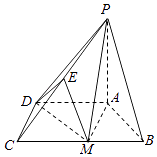
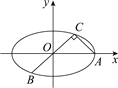
【题目】已知A,B,C是椭圆C: ![]() (a>b>0)上的三点,其中点A的坐标为(2
(a>b>0)上的三点,其中点A的坐标为(2![]() ,0),BC过椭圆的中心,且
,0),BC过椭圆的中心,且![]() ·
·![]() =0,|
=0,|![]() |=2|
|=2|![]() |
|
(1)求椭圆C的方程;
(2)过点(0,t)的直线l(斜率存在)与椭圆C交于P,Q两点,设D为椭圆C与y轴负半轴的交点,且|![]() |=|
|=|![]() |,求实数t的取值范围.
|,求实数t的取值范围.
【答案】(1)![]() +
+![]() =1. (2)
=1. (2) ![]()
【解析】试题分析:(1)根据点的坐标求出a,然后根据![]() 求出b,即可求出椭圆方程。(2)根据题意设出直线方程,与(1)中椭圆方程联立,设
求出b,即可求出椭圆方程。(2)根据题意设出直线方程,与(1)中椭圆方程联立,设![]() 运用违达定理运算,求出t的取值范围。
运用违达定理运算,求出t的取值范围。
试题解析:(1)由A的坐标为(2![]() ,0),所以
,0),所以![]() ,
, ![]() ,知OC=AC,所以C(
,知OC=AC,所以C(![]() ),代入椭圆方程,得b=2,所以椭圆标准方程:
),代入椭圆方程,得b=2,所以椭圆标准方程: ![]() 。
。
(2)显然,当直线k=0,时满足![]() ,此时-2<t<2,
,此时-2<t<2,
当直线![]() 时,设直线方程:y=kx+t,由
时,设直线方程:y=kx+t,由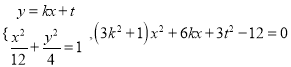 ,
,
设![]() ,PQ中点
,PQ中点![]() ,D(0,-2),
,D(0,-2), 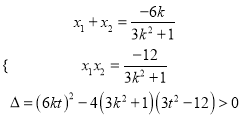 ,判别式化简得
,判别式化简得![]() ,得
,得![]() ,
, ![]() ,所以
,所以![]() ,代入
,代入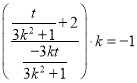 ,化简得
,化简得![]() ,代入
,代入![]() ,即
,即![]() ,所以
,所以![]()
综上所述, ![]()
![]()

练习册系列答案
相关题目