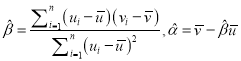题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
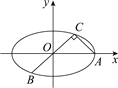
=1(a>b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
(1)求椭圆的标准方程
(2)设直线l:y=kx+1与椭圆C相交于P,Q两点,是否存在这样的实数k,使得以PQ为直径的圆过原点,若存在,请求出k的值:若不存在,请说明理由.
【答案】
(1)解:由题意得:  解得
解得 
所以椭圆的标准方程为 ![]()
(2)解:假设存在这样的实数k,使其满足题意,设P(x1,y1),Q(x2,y2)
联立方程组  ,
,
消去y得:(1+4k2)x2+8kx﹣12=0,
由题意得:x1、x2是此方程的解
所以 ![]() ∴
∴ ![]()
因为PQ为直径的圆过原点,
所以 ![]() ,即
,即 ![]()
解得 ![]() ,所以假设不成立,
,所以假设不成立,
所以,不存在这样的实数k,使得以PQ为直径的圆过原点
【解析】(1)利用已知条件列出列出求解椭圆的几何量求解椭圆的标准方程.(2)假设存在这样的实数k,使其满足题意,设P(x1 , y1),Q(x2 , y2),联立方程组  ,利用韦达定理,以及
,利用韦达定理,以及 ![]() ,转化求解即可.
,转化求解即可.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.

【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 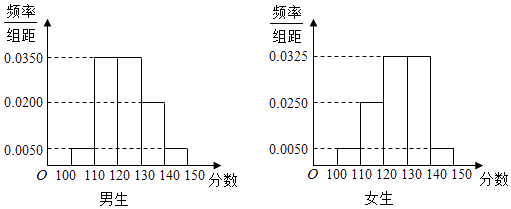
附:K2= ![]() .
.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |