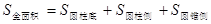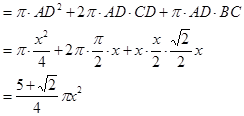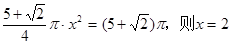题目内容
直角梯形的一个内角为45°，下底长为上底长的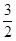
，这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是（
）
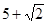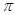，求这个旋转体的体积。
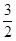，这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是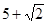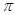（），求这个旋转体的体积。如图，梯形ABCD，AB//CD，∠A=90°，∠B=45°，绕AB边旋转一周后形成一圆柱和一圆锥的组合体。
设
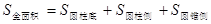
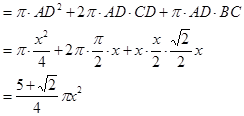
根据题设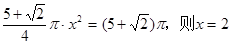
所以旋转体体积
设
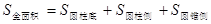
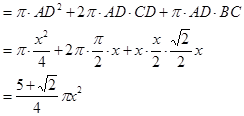
根据题设
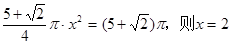
所以旋转体体积
略
练习册系列答案
相关题目
题目内容
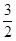，这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是（），求这个旋转体的体积。
所在平面与矩形
所在平面垂直，
，
=1，
，
是线段
的中点.
平面
；
的表面积；
，其余棱长都为1，其体积为
，则函数
中,
, 
,点
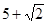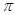是
的中点.
;
平面
;
的体积.
