题目内容
如图,AE是圆O的切线,A是切线, 于
于 ,割线EC交圆O于B,C两点.
,割线EC交圆O于B,C两点.

(1)证明:O,D,B,C四点共圆;
(2)设 ,
, ,求
,求 的大小.
的大小.
 于
于 ,割线EC交圆O于B,C两点.
,割线EC交圆O于B,C两点.
(1)证明:O,D,B,C四点共圆;
(2)设
 ,
, ,求
,求 的大小.
的大小.(1)证明过程详见解析;(2) .
.
 .
.试题分析:本题以圆为几何背景考查边和角的关系、四点共圆等基础知识,考查学生的转化能力.第一问,连结OA,由于AE为圆的切线,所以
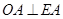 ,又根据射影定理,得
,又根据射影定理,得 ,再由切割线定理得
,再由切割线定理得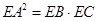 ,所以得到
,所以得到 ,因为
,因为 与
与 有一公共角,所以
有一公共角,所以 与
与 相似,所以
相似,所以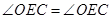 ,所以利用四点共圆的判定得证;第二问,由
,所以利用四点共圆的判定得证;第二问,由 的内角和为
的内角和为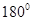 ,再结合第一问得到的
,再结合第一问得到的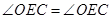 进行角的转换即可求出
进行角的转换即可求出 的大小.
的大小.试题解析:(1)连结
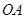 ,则
,则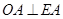 .由射影定理得
.由射影定理得 .
.由切割线定理得
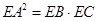 ,故
,故 ,即
,即 ,
,又
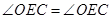 ,所以
,所以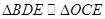 ,所以
,所以 .
.因此
 四点共圆. 6分
四点共圆. 6分(2)连结
 .因为
.因为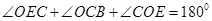 ,
,
结合(1)得
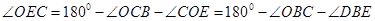
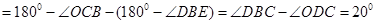 . 10分
. 10分
练习册系列答案
相关题目
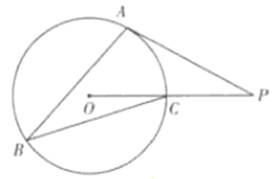
 AC,AE=
AC,AE= AB,BD,CE相交于点F.
AB,BD,CE相交于点F.

 中,
中, ,
, ,
, ,
, 、
、 为垂足,若AE=4,BE=1,则AC= .
为垂足,若AE=4,BE=1,则AC= .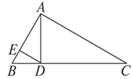


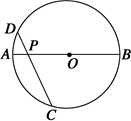
 切圆
切圆 于点
于点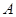 ,割线
,割线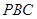 经过圆心
经过圆心 ,
, 绕点
绕点 到
到 ,则
,则 的长为 .
的长为 .