题目内容
如图所示,圆O的半径为1,A、B、C是圆周上的三点,满足∠ABC=30°,过点A做圆O的切线与OC的延长线交于点P,则PA=_____________.
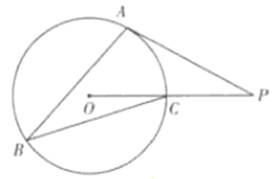

法一:连接OA得∠AOP=60°(同弧所对的圆周角是圆心角的一半)
因为PA与圆相切,所以∠OAP=90°,所以∠P=30°,
因为OA="1," 所以OP=2,由勾股定理知,PA=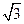

法二:延长PO交圆于点D,连接AD、OA(如图),则∠D=∠B=30°,
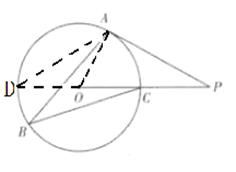
因为OA=OD,所以∠DAO=∠D=30°,
又因为OA⊥PA,所以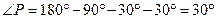 ,所以PA=AD,
,所以PA=AD,
在△AOD中,由余弦定理得,AD=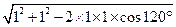 =
=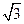 ,
,
故PA=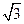
因为PA与圆相切,所以∠OAP=90°,所以∠P=30°,
因为OA="1," 所以OP=2,由勾股定理知,PA=
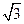

法二:延长PO交圆于点D,连接AD、OA(如图),则∠D=∠B=30°,

因为OA=OD,所以∠DAO=∠D=30°,
又因为OA⊥PA,所以
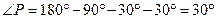 ,所以PA=AD,
,所以PA=AD,在△AOD中,由余弦定理得,AD=
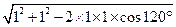 =
=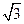 ,
,故PA=

练习册系列答案
相关题目
 于
于 ,割线EC交圆O于B,C两点.
,割线EC交圆O于B,C两点.
 ,
, ,求
,求 的大小.
的大小.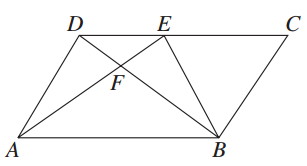

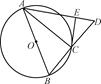
 .
.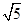 ,则AB=________.
,则AB=________.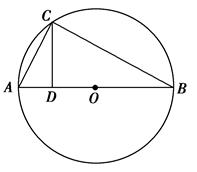
 ,
, ,则CP= .
,则CP= .