题目内容
13.下列说法中正确的是( )| A. | 命题“若x>y,则-x<-y”的逆否命题是“若-x>-y,则x<y” | |
| B. | 若命题p:?x∈R,x2+1>0,则¬p:?x∉R,x2+1≤0 | |
| C. | 设x、y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 | |
| D. | 设l是一条直线,α、β是两个不同的平面,若l⊥α,l⊥β,则α∥β |
分析 写出原命题的逆否命题,可判断A;写出原命题的否定,可判断B;根据充要条件的定义,可判断C;根据线面垂直的性质,可判断D.
解答 解:A中,命题“若x>y,则-x<-y”的逆否命题是“若-x≥-y,则x≤y”,故A错误;
B中,若命题p:?x∈R,x2+1>0,则¬p:?x∈R,使x2+1≤0,故B错误;
C中,设x、y∈R,则“(x-y)•x2<0”⇒“x<y且x≠0”,充分性成立,反之,不可,即必要性不成立,故C错误;
D中,设l是一条直线,α、β是两个不同的平面,若l⊥α,l⊥β,则α∥β,故D正确;
故选:D.
点评 本题以命题的真假判断为载体考查了四种命题,命题的否定,充要条件,空间线面关系等知识点,难度不大,属于基础题.

练习册系列答案
相关题目
18.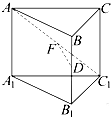 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.设a∈R,若函数y=ex+2ax,x∈R有大于0的极值点,则( )
| A. | a<-$\frac{1}{e}$ | B. | a>-$\frac{1}{e}$ | C. | a<-$\frac{1}{2}$ | D. | a>-$\frac{1}{2}$ |
16.某中学有甲乙两个文科班进行数学考试,按照大于或等于120分为优秀,120分以下为非优秀统计成绩后,得到如下列联表:
(Ⅰ)用分层抽样的方法在优秀的学生中抽6人,其中甲班抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰有一名同学在乙班的概率;
(Ⅲ)计算出统计量k2,若按95%可靠性要求能否认为“成绩与班级有关”.
下面的临界值表代参考:
(参考公式k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)在上述抽取的6人中选2人,求恰有一名同学在乙班的概率;
(Ⅲ)计算出统计量k2,若按95%可靠性要求能否认为“成绩与班级有关”.
下面的临界值表代参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |