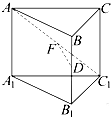在棱长均相等的正三棱柱ABC-A1B1C1中.D为BB1的中点.F在AC1上.且DF⊥AC1.则下述结论:①AC1⊥BC,②AF=FC1,③平面DAC1⊥平面ACC1A1.其中正确的个数为( )A．0B．1C．2D．3 题目和参考答案——青夏教育精英家教网—

题目内容

18．

在棱长均相等的正三棱柱ABC-A₁B₁C₁中，D为BB₁的中点，F在AC₁上，且DF⊥AC₁，则下述结论：①AC₁⊥BC；②AF=FC₁；③平面DAC₁⊥平面ACC₁A₁，其中正确的个数为（　　）

A．

B．

C．

D．

分析设出棱长，通过直线与直线的垂直判断直线与直线的平行，推出①的正误；判断F是AC₁的中点推出②正误；利用直线与平面垂直推出排名与平面垂直推出③正误；

解答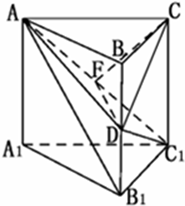解：不妨设棱长为：2，对于①连结AB₁，则AB₁=AC₁=2$\sqrt{2}$，∴∠AC₁B₁≠90°即AC₁与B₁C₁不垂直，又BC∥B₁C₁，∴①不正确；
对于②，连结AD，DC₁，在△ADC1中，AD=DC₁=$\sqrt{5}$，而DF⊥AC₁，∴F是AC₁的中点，AF=FC₁；∴②正确；
对于③由②可知，在△ADC₁中，DF=$\sqrt{3}$，连结CF，易知CF=$\sqrt{2}$，而在Rt△CBD中，CD=$\sqrt{5}$，∴DF²+CF²=CD²，
即DF⊥CF，又DF⊥AC₁，∴DF⊥面ACC₁A₁，∴平面DAC₁⊥平面ACC₁A₁，∴③正确；
故选：C．

点评本题考查命题的真假的判断，棱锥的结构特征，直线与平面垂直，直线与直线的位置关系的应用，考查空间想象能力以及逻辑推理能力．

练习册系列答案

启东系列江苏省13大市中考真题汇编系列答案

江苏13大市中考20套卷系列答案

润学书业亮点给力江苏中考48套系列答案

锁定中考江苏十三大市中考试卷汇编系列答案

名校压轴题系列答案

9．已知向量$\overrightarrow{a}$=（cos$\frac{3x}{2}$，sin$\frac{3x}{2}$），$\overrightarrow{b}$=（cos$\frac{x}{2}$，-sin$\frac{x}{2}$），且x∈[0，$\frac{π}{2}$]．
（1）求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|；
（2）若f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值是-2，求λ的值．

6．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，过F₂的直线交双曲线的右支于A，B两点，若△ABF₁是以A为直角顶点的等腰三角形，e为双曲线的离心率，则e²=5-2$\sqrt{2}$．

13．下列说法中正确的是（　　）

	A．	命题“若x＞y，则-x＜-y”的逆否命题是“若-x＞-y，则x＜y”
	B．	若命题p：?x∈R，x²+1＞0，则￢p：?x∉R，x²+1≤0
	C．	设x、y∈R，则“（x-y）•x²＜0”是“x＜y”的必要而不充分条件
	D．	设l是一条直线，α、β是两个不同的平面，若l⊥α，l⊥β，则α∥β

3．方程|x²-2x-3|=m有4个解，求m的取值范围．

4．已知椭圆M：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，短半轴长是1
（1）求椭圆M的方程
（2）已知C是椭圆M上异于左、右顶点A，B的一动点，作CD⊥x轴于点D，延长DC到点E，使得|DC|=|CE|，直线BE交直线x=-2于点F，AF的中点是G，试判断直线GE与以AB为直径的圆的位置关系．

1．若在散点图中，所有的样本点都落在一条斜率为非0实数的直线上，则相关指数R²=1．

2．已知log₃（log₂x）=1，则${x}^{\frac{1}{2}}$=（　　）

A．

2$\sqrt{2}$

B．

$\frac{1}{2\sqrt{2}}$

C．

$\frac{1}{2\sqrt{3}}$

D．

2$\sqrt{3}$

试题分类