题目内容
3.已知奇函数f(x)、偶函数g(x)满足f(x)+g(x)=ax(a>0且a≠1).(1)求函数f(x)和g(x)的解析式;
(2)求使f(2x)=mf(x)g(x)恒成立的实数m的值;
(3)探究y=f(x)的单调性,并用单调性的定义证明.
分析 (1)运用奇偶性的定义,将x换成-x,运用函数方程的思想,可得f(x),g(x)的解析式;
(2)运用指数的运算性质,计算即可得到m=2;
(3)当a>1时,f(x)在R上递增,当0<a<1时,f(x)在R上递减.运用单调性的定义,注意作差、变形和定符号和下结论,几个步骤.
解答 解:(1)f(x)+g(x)=ax(a>0且a≠1).①
可得f(-x)+g(-x)=a-x,
由奇函数f(x)、偶函数g(x),可得f(-x)=-f(x),g(-x)=g(x),
即有-f(x)+g(x)=a-x,②
由①②可得,f(x)=$\frac{1}{2}$(ax-a-x),
g(x)=$\frac{1}{2}$(ax+a-x);
(2)f(2x)=$\frac{1}{2}$(a2x-a-2x),
f(x)g(x)=$\frac{1}{4}$(a2x-a-2x),
由f(2x)=mf(x)g(x)恒成立,可得m=2;
(3)当a>1时,f(x)在R上递增,当0<a<1时,f(x)在R上递减.
证明如下:设m<n,则f(m)-f(n)=$\frac{1}{2}$(am-a-m)-$\frac{1}{2}$(an-a-n)
=$\frac{1}{2}$[(am-an)+$\frac{{a}^{m}-{a}^{n}}{{a}^{m+n}}$]=$\frac{1}{2}$(am-an)(1+$\frac{1}{{a}^{m+n}}$),
当a>1时,0<am<an,即有f(m)-f(n)<0,即为f(m)<f(n);
当0<a<1时,am>an,即有f(m)-f(n)>0,即为f(m)>f(n).
即有当a>1时,f(x)在R上递增,当0<a<1时,f(x)在R上递减.
点评 本题考查函数的性质和应用,主要考查函数的奇偶性和单调性的运用,同时考查指数函数的单调性和应用,属于中档题.

| A. | x-2y=0 | B. | 2x-y-3=0 | C. | x-y+1=0 | D. | x-y-1=0 |
| A. | 外切 | B. | 内切 | C. | 相离 | D. | 相交 |
| A. | 命题“若x>y,则-x<-y”的逆否命题是“若-x>-y,则x<y” | |
| B. | 若命题p:?x∈R,x2+1>0,则¬p:?x∉R,x2+1≤0 | |
| C. | 设x、y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 | |
| D. | 设l是一条直线,α、β是两个不同的平面,若l⊥α,l⊥β,则α∥β |

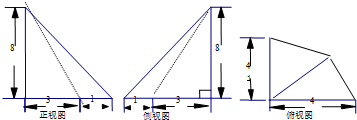 已知某空间几何体的三视图如图所示,则该几何体的体积是32.
已知某空间几何体的三视图如图所示,则该几何体的体积是32.