题目内容
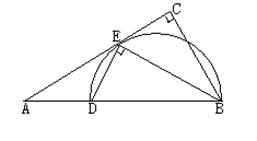
如图,在Rt△ABC中,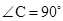 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,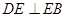 .
.
(1)求证:AC是△BDE的外接圆的切线;
(2)若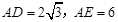 ,求EC的长.
,求EC的长.
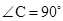 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,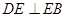 .
.(1)求证:AC是△BDE的外接圆的切线;
(2)若
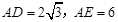 ,求EC的长.
,求EC的长.
(1)见解析;(2)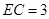
试题分析:(1)欲证
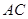 为
为 的外接圆切线,利用“弦切角与同弦所对的圆周角相等”性质,若能证明
的外接圆切线,利用“弦切角与同弦所对的圆周角相等”性质,若能证明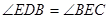 ,则可证结论,方法二:取
,则可证结论,方法二:取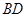 的中点为
的中点为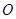 ,若能证
,若能证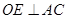 ,则结论也成立(自行证明);(2)根据切割线定理(圆幂定理之一),可得
,则结论也成立(自行证明);(2)根据切割线定理(圆幂定理之一),可得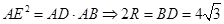 ,并利用(1)中所证得
,并利用(1)中所证得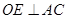 ,利用三角形
,利用三角形 ,可求得
,可求得 .
.试题解析:
证明:
因为在Rt△ABC中,
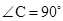 , 点D在AB上,
, 点D在AB上,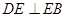 .
.所以DB是
 的外接圆直径,
的外接圆直径,又因为BE平分∠ABC交AC于点E,
故
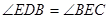 ,
,故AC是△BDE的外接圆的切线. 4分
设BD的中点为O,连接OE,
由(1)知则OE
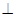 AC,从而
AC,从而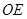 ‖BC,
‖BC,又
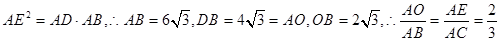 ,
,从而AC=9.,得EC=3 .10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 O外一点,PA是切线,A为切点,割线PBC与
O外一点,PA是切线,A为切点,割线PBC与
 DE=2
DE=2
 的直径
的直径 ,
, 是
是 延长线上的一点,过
延长线上的一点,过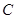 ,连接
,连接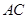 ,若
,若 ,
,
 .
.