题目内容
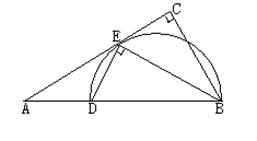
如图,过抛物线y2=2px(p>0)的顶点作两条互相垂直的弦OA、OB.
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹方程.
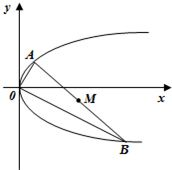
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹方程.

(1)∵依题意可知直线OA的斜率存在且不为0
∴设直线OA的方程为y=kx(k≠0)
∴联立方程
解得xA=
,yA=
(4分)
以-
代上式中的k,解方程组
,解得xB=2pk2,yB=-2pk
∴A(
,
),B(2pk2,-2pk)(8分)
(2)设AB中点M(x,y),则由中点坐标公式,得
(10分)
消去参数k,得y2=px-2p2;即为M点轨迹的普通方程.(12分)
∴设直线OA的方程为y=kx(k≠0)
∴联立方程
|
| 2p |
| k2 |
| 2p |
| k |
以-
| 1 |
| k |
|
∴A(
| 2p |
| k2 |
| 2p |
| k |
(2)设AB中点M(x,y),则由中点坐标公式,得
|
消去参数k,得y2=px-2p2;即为M点轨迹的普通方程.(12分)

练习册系列答案
相关题目
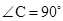 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,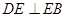 .
.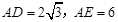 ,求EC的长.
,求EC的长.